* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Solving Equations - Etiwanda E
Survey
Document related concepts
Transcript
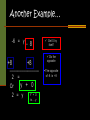
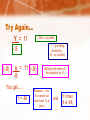
Solving Equations What??? Why??? How??? By: Lori Edwards What Will I Learn? solve equations using equality properties. Solve equations using both equality properties Why Should I Learn Algebra? To get a job. Not all jobs using algebra are boring! Fun jobs Computer programmer Chef Airplane maintenance Nurse Shopping specialist Comparing Solving Equations to Real Life Situations! Be FAIR!!! My brother got more. Not fair or equal. Scales –one side is heavier, both sides don’t weigh the same. What Skills Do I Need To Know? What does opposite mean: (+/-) (x/÷) +, -, x, and ÷ Integers The Addition Property of Equality X +5 = 7 - 5 -5 ________________ X + 0 = 2 Or X+0 is…X X =2 Get X by itself Do the opposite The opposite of + 5 is - 5 Another Example… -6 = y - 8 +8 +8 _______________ 2 = y + 0 Or Y + 0 2 = y is ….y Get X by itself Do the opposite The opposite of -8 is +8 The Multiplication Property of Equality - 12 x = 72 ______ _____ -12 -12 X = -6 Get x by itself The opposite of multiplying is dividing -12 ÷ -12 = 1 (you are left with only 1x) 72 ÷ -12 = - 6 Try Again… Get x by itself Y = 11 -8 (-8) (y is being divided by 8)…so multiply y = 11 (-8) -8 You get….. Y = -88 Multiply both sides of the equation by -8 Because… the 8’s cancel out and leave 1y or just y and 11 times -8 is -88 Using Both Properties! - 5X + 6 = -16 -6 -6 Get x by itself Get rid of the +6 by subtracting Get rid of the -5 by dividing ____________________________ -5x -5 You are left with… x = +22 5 = - 22 -5 Fun Facts!!! Works cited