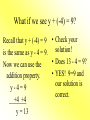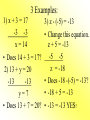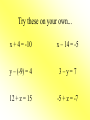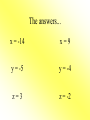Download Notes (ver 2):Solving Equations by Addition or Subtraction

Solving Equations Using
Addition and Subtraction
Objectives:
• A.4f Apply these skills to solve practical
problems.
• A.4b Justify steps used in solving equations.
• Use a graphing calculator to check your
solutions.
To Solve an Equation means...
• To isolate the variable having a
coefficient of 1 on one side of the
equation.
• Ex: x = 5 is solved for x.
• y = 2x - 1 is solved for y.
Addition Property of Equality
For any numbers a, b, and c, if
a = b, then a + c = b + c.
What it means:
You can add any number to
BOTH sides of an equation and
the equation will still hold true.
An easy example:
• Would you ever
We all know that 7 = 7. leave the house
with only one shoe
on?
Does 7 + 4 = 7? NO!
• Would you ever put
blush on just one
But 7 + 4 = 7 + 4.
cheek?
The equation is still
• Would you ever
true if we add 4
shave just one side
of your face?
to both sides.
Let’s try another example!
x - 6 = 10
Add 6 to each
side.
x - 6 = 10
+6 +6
x = 16
• Always check your
solution!!
• The original problem
is x - 6 = 10.
• Using the solution
x=16,
Does 16 - 6 = 10?
• YES! 10 = 10 and our
solution is correct.
What if we see y + (-4) = 9?
Recall that y + (-4) = 9 • Check your
solution!
is the same as y - 4 = 9.
•
Does
13
4
=
9?
Now we can use the
• YES! 9=9 and
addition property.
our
solution
is
y-4=9
correct.
+4 +4
y = 13
How about -16 + z = 7?
• Remember to always • Check you solution!
use the sign in front
of the number.
• Does -16 + 23 = 7?
• Because 16 is
negative, we need to
add 16 to both sides. • YES! 7 = 7 and our
solution
is
correct.
• -16 + z = 7
+16
+16
z = 23
A trick question...
-n - 10 = 5
+10 +10
-n = 15
• Do we want -n? NO,
we want positive n.
• If the opposite of n
is positive 15, then n
must be negative 15.
• Solution: n = -15
• Check your
solution!
• Does -(-15)-10=5?
• Remember, two
negatives = a
positive
• 15 - 10 = 5 so our
solution is correct.
Subtraction Property of Equality
• For any numbers a, b, and c,
if a = b, then a - c = b - c.
What it means:
• You can subtract any number from
BOTH sides of an equation and the
equation will still hold true.
3 Examples:
1) x + 3 = 17
-3 -3
x = 14
• Does 14 + 3 = 17?
2) 13 + y = 20
-13
-13
y=7
• Does 13 + 7 = 20?
3) z - (-5) = -13
• Change this equation.
z + 5 = -13
-5 -5
z = -18
• Does -18 -(-5) = -13?
• -18 + 5 = -13
• -13 = -13 YES!
Try these on your own...
x + 4 = -10
x – 14 = -5
y – (-9) = 4
3 – y= 7
12 + z = 15
-5 + z = -7
The answers...
x = -14
x=9
y = -5
y = -4
z=3
z = -2