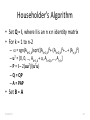Download AlgEV Problem - Govt College Ropar

ALGEBRAIC EIGEN VALUE
PROBLEMS
ALGEBRAIC EIGEN VALUE PROBLEMS
Ax  x
square matrix
unknown vector
unknown scalar
x = 0: (no practical interest)
x  0: eigenvectors of A; exist only for certain values of  (eigenvalues or
characteristic roots)
 Multiplication of A = same effect as the multiplication of x by a scalar 
- Eigenvalue: special set of scalars associated with a linear systems of equations.
Each eigenvalue is paired with a corresponding eigenvectors.
Eigenvalues, Eigenvectors
- Eigenvalue problems: A x   x or
A  I x  0
eigenvectors
eigenvectors
Set of eigenvalues: spectrum of A
Largest of i : spectral radius of A
How to Find Eigenvalues and Eigenvectors
Ex. 1.)
 5 2 
A

2

2


 5x 1  2 x 2  x 1
2 x 1  2 x 2  x 2
A  Ix  0
In homogeneous linear system, nontrivial solutions exist when det (A-I)=0.
Characteristic equation of A:
5
2
D()  det( A   I) 
 2  7  6  0
2
2
Characteristic polynomial
Characteristic determinant
Eigenvalues: 1=-1 and 2= -6
Eigenvectors: for 1=-1,
obtained from Gauss elimination
1 
x1   
 2
for 2=-6,
2
x2   
 1
General Case
a11x1  a12 x 2    a1n x n  x1

a n1x1  a n 2 x 2    a nn x n  x n
A  I x  0,
D()  det A   I   0
Theorem 1:
Eigenvalues of a square matrix A  roots of the characteristic equation of A.
nxn matrix has at least one eigenvalue, and at most n numerically different eigenvalues.
Theorem 2:
If x is an eigenvector of a matrix A, corresponding to an eigenvalue ,
so is kx with any k0.
Ex. 2) multiple eigenvalue
- Algebraic multiplicity of : order M of an eigenvalue 
Geometric multiplicity of : number of m of linear independent eigenvectors
corresponding to . (=dimension of eigenspace of )
Defect of : =M-m
In general, m  M
Ex 3) algebraic & geometric multiplicity, positive defect
Ex. 4) complex eigenvalues and eigenvectors
Some Applications of Eigenvalue Problems
Ex. 1) Stretching of an elastic membrane.
Find the principal directions: direction of position vector x of P
= (same or opposite) direction of the position vector y of Q
 y   5 3   x1 
  
x12  x 22  1, y   1   
 y 2   3 5 x 2 
1
y  A x   x  1  8, x1 for 1   
1
1
2  2, x 2 for 2   
  1
Eigenvalue represents speed of response
Eigenvector ~ direction
Ex. 4) Vibrating system of two masses on two springs
y1''  5 y1  2 y 2
y '2'  2 y1  2 y 2
Solution vector:
y  xe wt
 A x   x (  w 2 ) solve eigenvalues and eigenvectors
 y  x1 (a1 cos t  b1 sin t )  x 2 (a 2 cos 6t  b 2 sin 6t )
Examples for stability analysis of linear ODE systems using eigenmodes
Stability criterion: signs of real part of eigenvalues of the matrix
x 
dx
 Ax
dt
A determine the stability of the linear system.
Re() < 0: stable
Re() > 0: unstable
Ex. 1) Node-sink
x 1  0.5x1  x 2  1  0.5
x 2  2x 2
2  2
stable
Ex. 2) Saddle
0.2703 
x 1  2 x1  x 2  1  1.5616 , x1 for 1  
unstable
  0.9628 


x 2  2 x1  x 2
 0.8719 
Phase plane ?

2  2.5616 , x 2 for 2  
 0.4896 
Ex. 3) Unstable focus
x 1  x1  2x 2  1  1  2i
x 2  2x1  x 2
2  1  2i
unstable
Phase plane ?
Ex. 4) Center
x 1   x1  x 2  1  0  1.7321i
x 2  4x1  x 2
2  0  1.7321i
Properties of Eigenvalue
1) Trace
2) det
n
n
i 1
i 1
A   aii   i
n
A   i
i 1
3) If A is symmetric, then the eigenvectors are
i j
 0,
orthogonal:
T
xi x j  
i j
Gii
4) Let the eigenvalues of
A  1 , 2 ,n
then, the eigenvalues of (A - aI)
 1  a, 2  a,, n  a,
• Transformation
Ax
Ax  x : The transformation of an eigenvector
is mapped onto the same line of.
Geometrical Interpretation of Eigenvectors
• Symmetric matrix  orthogonal eigenvectors
• Relation to Singular Value
if A is singular  0
{eigenvalues}
Similar Matrices
• Eigenvalues and eigenvectors of similar
matrices
Eg. Rotation matrix
contents
•
•
•
•
•
•
Jacobi’s method
Given’s method
House holder’s method
Power method
QR method
Lanczo’s method
Jacobi’s Method
• Requires a symmetric matrix
• May take numerous iterations to converge
• Also requires repeated evaluation of the
arctan function
• Isn’t there a better way?
• Yes, but we need to build some tools.
Jacobi method idea
Find large off-diagonal element a p , q .
Set it to zero using R p ,q ( ) .
Since ãp , q =(ap , q - a p , p )sinθcosθ+a p , q (cos 2 ø – sin2 ø),
Set
tan 2 
2a p , q
a p , p  aq ,q
The Jacobi Algorithm
• One of the oldest numerical methods, but still of
interest
• Start with initial guess at V (e.g. V=I), set A=VTAV
• For k=1, 2, …
– If A is close enough to diagonal (Frobenius norm of offdiagonal tiny relative to A) stop
– Find a Givens rotation Q that solves a 2x2 subproblem
• Either zeroing max off-diagonal entry, or sweeping in order
through matrix.
– V=VQ, A=QTAQ
• Typically O(log n) sweeps, O(n2) rotations each
• Quadratic convergence in the limit
cs542g-term1-2006
14
• Example
1 1 8 


A  1 2 2
8 2 1


• pick another big off-diagonal element: repeat.
• PROBLEM: zero elements are made nonzero
• again.
Givens method idea
• Take off-diagonal element
a p ,q , p  q  2
• Set it to zero using
R p 1,q ( )
since
set
a p ,q  a p, p 1 sin   a p,q cos  ,
tan  
a p ,q
a p , p 1
• Example
1

8

A
8

3
8
2
5
4
8
5
3
1
3

4
1

1
• Work through elements in turn
• (p, q) = (1, 3), (1, 4), . . . , (1, n), (2, 4), (2, 5),. . .(2, n), (3, 1),.. (n − 3, n − 1),
(n − 3, n),….(n − 2, n).
• PROBLEM: This cannot reduce beyond tridiagonal form.
Givens Method
• – based on plane rotations
• – reduces to tridiagonal form
• – finite (direct) algorithm
What Householder’s Method Does
• Preprocesses a matrix A to produce an upperHessenberg form B
• The eigenvalues of B are related to the
eigenvalues of A by a linear transformation
• Typically, the eigenvalues of B are easier to
obtain because the transformation simplifies
computation
House holder method
• – based on an orthogonal transformation
• – reduces to tridiagonal form
• – finite (direct) algorithm
Definition: Upper-Hessenberg Form
• A matrix B is said to be in upper-Hessenberg
form if it has the following structure:
 b1,1 b1,2
b b
 2,1 2,2
 0 b3,2
B
0 0
 


 0 0
b1,3
b 2,3
b3,3
b 4,3







0
b1,n -1 b1,n 
b 2,n -1 b 2,n 
b3,n -1 b3,n 


 
b n -1,n -1 b n -1,n 

b n,n -1 b n,n 
A Useful Matrix Construction
• Assume an n x 1 vector u  0
• Consider the matrix P(u) defined by
P(u) = I – 2(uuT)/(uTu)
• Where
– I is the n x n identity matrix
– (uuT) is an n x n matrix, the outer product of u
with its transpose
– (uTu) here denotes the trace of a 1 x 1 matrix and
is the inner or dot product
5/24/2017
22
Properties of P(u)
• P2(u) = I
– The notation here P2(u) = P(u) * P(u)
– Can you show that P2(u) = I?
• P-1(u) = P(u)
– P(u) is its own inverse
• PT(u) = P(u)
– P(u) is its own transpose
– Why?
• P(u) is an orthogonal matrix
5/24/2017
23
Householder’s Algorithm
• Set Q = I, where I is an n x n identity matrix
• For k = 1 to n-2
– a = sgn(Ak+1,k)sqrt((Ak+1,k)2+ (Ak+2,k)2+…+ (An,k)2)
– uT = [0, 0, …, Ak+1,k+ a, Ak+2,k,…, An,k]
– P = I – 2(uuT)/(uTu)
– Q = QP
– A = PAP
• Set B = A
5/24/2017
24
Example
 1 2 3
Let A  3 5 6 .
4 8 9 3 x 3
Clearly, n  3 and since n - 2  1, k takes only the value k  1.
2
2
Then a  sgn(a 21 ) a21
 a31
 sgn(3 ) 32  4 2  1 5  5
Example
uT  [0,...,0, a21  a , a31,..., an1 ]  [0, a21  a , a31 ]
 [0,3  5,4]  [0,8,4]
0 
80 8 4
 
1
0
0


4
uu T 

P  I  2 T  0 1 0   2
?
u u
0 
0 0 1
0 8 48
4
Example
0 
80 8 4
 
1 0 0
T
 4
uu
P  I  2 T  0 1 0  2  
u u
0 
0 0 1
0 8 48
4


0 
1 0 0
0 0 0  1 0

2 
 3  4



2
 0 1 0  0 64 32  0
. Find P  ?
80
5
5 
0 0 1
0 32 16  
0  4 3 

5
5 
Example
Initially, Q  I, so

1 0 0 1



Q  QP  0 1 0 0
0 0 1 
0

0
3
5
4
5
 
0  1
 4 
  0
5  
3  
0


5  
0
3
5
4
5

0 
 4

5 
3 
5 
Example
Next, A  PAP , so

1

A  0

0

0
3
5
4
5


0  1 2 3 1

 4 

  3 5 6  0
5 



4
8
9
3 

0


5 

0
3
5
4
5

0 
 4
?
5 
3 
5 
Example
Hence,

1

A  0

0


1

 - 5

0

0
3
5
4
5
- 18
5
357
25
- 24
25


0  1 2 3 1

 4 

  3 5 6  0
5 

3  4 8 9 
0


5 

1
5
26 

25 
-7
25 
0
3
5
4
5
 
0  1
 4 
   5
5  
3  
0


5  
2
 47
5
4
5

3  1
 54  
 0
5 
3 
0


5 
0
3
5
4
5

0 
 4

5 
3 
5 
Example
Finally, since the loop only executes once
- 18

1
5

357
B  A  - 5
25

 0 - 24

25
So what?
1
5
26 
.
25 
-7
25 
How Does It Work?
• Householder’s algorithm uses a sequence of similarity
transformations
B = P(uk) A P(uk)
to create zeros below the first sub-diagonal
• uk=[0, 0, …, Ak+1,k+ a, Ak+2,k,…, An,k]T
• a = sgn(Ak+1,k)sqrt((Ak+1,k)2+ (Ak+2,k)2+…+ (An,k)2)
• By definition,
– sgn(x) = 1, if x≥0 and
– sgn(x) = -1, if x<0
How Does It Work? (continued)
• The matrix Q is orthogonal
– the matrices P are orthogonal
– Q is a product of the matrices P
– The product of orthogonal matrices is an
orthogonal matrix
• B = QT A Q hence Q B = Q QT A Q = A Q
– Q QT = I (by the orthogonality of Q)
How Does It Work? (continued)
• If ek is an eigenvector of B with eigenvalue k,
then B ek = k ek
• Since Q B = A Q,
A (Q ek) = Q (B ek) = Q (k ek) = k (Q ek)
• Note from this:
– k is an eigenvalue of A
– Q ek is the corresponding eigenvector of A
The Power Method
• Start with some random vector v, ||v||2=1
• Iterate v=(Av)/||Av||
• What happens? How fast?
35
The QR Method: Start-up
• Given a matrix A
• Apply Householder’s Algorithm to obtain a
matrix B in upper-Hessenberg form
• Select e>0 and m>0
– e is a acceptable proximity to zero for subdiagonal elements
– m is an iteration limit
The QR Method: Main Loop
Do {
Set Q T  I
For k  1 to n - 1{
c
Bk ,k
2
k ,k
B
B
2
k 1, k
; s
Bk 1,k
2
k ,k
B
B
2
k 1, k
;
Set P  I; Pk,k  Pk 1,k 1  c; Pk 1,k  Pk,k 1  s;
B  PB ;
Q T  PQ T ;
}
B  BQ;
i  ;
} While (B is not upper block tria ngular) and (i  m)
The QR Method: Finding The ’s
Since B is upper block tria ngular, one may compute k from
the diagonal blocks of B. Specifical ly, the eigvalues of B are
the eigenvalue s of its diagonal blocks B k .
If a diagonal block B k is 1x1, i.e., B k  a , then k  a.
a b 
If a diagonal block B k is 2x2, i.e., B k  
,

c d 
trace(B k )  trace2 (B k )  4 det( B k )
then k ,k 1 
.
2
Details Of The Eigenvalue Formulae
a b 
Suppose B k  
.

c d 
  a  b 
I  B k  

 c   d
I  B k  ?
5/24/2017
39
Details Of The Eigenvalue Formulae
  a  b 
Given I  B k  

 c   d
I  B k  (  a)(  d )  bc
   (a  d )  ad  bc
2
   trace(B k )  det( B k )
2
5/24/2017
40