* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Exit Level
Survey
Document related concepts
Transcript
Exit Level
TAKS Preparation Unit
Objective 2
© A Very Good Teacher 2007
Parent Functions
• There are two parent functions on the
TAKS test:
Linear
Quadratic
y = x²
y=x
Opens up
Vertex at (0, 0)
y axis is axis of
symmetry
2, Ab2A
© A Very Good Teacher 2007
Domain and Range
• Domain is the set of all x values
• Range is the set of all y values
• To find domain: examine the right and left
boundaries of the function
• To find range: examine the top and bottom
boundaries of the function
• Whenever a function has two boundaries,
both signs should be less than (< or ≤).
2, Ab2B
© A Very Good Teacher 2007
Domain and Range, cont…
• Example of finding the Domain
Domain:
____ < x ≤ ____
-3
2
2, Ab2B
© A Very Good Teacher 2007
Domain and Range, cont…
• Example of finding the Range
5
Range
____ ≤ y < ____
-4
2, Ab2B
© A Very Good Teacher 2007
Interpreting Graphs
• Pay attention to labels on x and y axes
• A straight line indicates constant rate
of change (slope)
• A curved line indicates a changing rate
• More than one straight lines indicates
rapidly changing constant rates
2, Ab2C
© A Very Good Teacher 2007
Interpreting Graphs, cont…
• The slope of lines indicates speed
– Steep line means rapid speed
– Flat line means no movement
No movement
1000 ft in 1 min
fastest speed
1000 ft in 2 min
or 500 ft per min
500 ft in 2 min
or 250 ft per min
500 ft in 1 min
2, Ab2C
© A Very Good Teacher 2007
Scatter Plots
Correlation
Positive
Negative
2, Ab2D
No
© A Very Good Teacher 2007
Using symbols
• Focus on the meaning of words in a
mathematical context
• For Example:
More, more than, in addition, …. Mean … +
Less, less than, difference …. Mean … Times, per, each, …
Mean … x
Per, each, dividend …
Mean … ÷
Is or other verbs …
Mean … =
The goal is to turn a sentence into an equation.
3, Ac3A
© A Very Good Teacher 2007
Using symbols, cont…
Here is a simple example:
The area of a circle is equivalent to pi times the
radius squared.
A
= π • r ²
So, you would look for the answer A = πr²
3, Ac3A
© A Very Good Teacher 2007
Patterns
•
Given a geometric sequence,
you must determine the equation
for the function.
1. Make a table to represent the
sequence
2. Use STAT to calculate the
answer
3. Find the answer that fits the
calculator answer
3, Ac3B
© A Very Good Teacher 2007
Patterns, cont…
• Here’s an example: Make a table
Figure
# of
squares
1
2
3
4
1
4
9
16
3, Ac3B
© A Very Good Teacher 2007
Patterns, cont…
• Now use STAT to calculate the equation.
STAT
ENTER
NUMBERS
STAT
5, ENTER
Look for an answer that has
an equation like y = x².
3, Ac3B
© A Very Good Teacher 2007
Solving Equations and Inequalities
• Substitute given values
• Use inverse operations to solve
• Example: If (2.25, y) is a solution to the
equation 4x – 2y = 8, what is the value of y?
4x – 2y = 8
4(2.25) – 2y = 8
y=½
9 – 2y = 8
-9
-9
– 2y = -1
-2 -2
3, Ab4A
© A Very Good Teacher 2007
Solving Equations and Inequalities, cont…
• Convert inequalities from Standard form (Ax +
By > C) to y = mx + b form.
• Use the same steps as you would for an equation, but
remember that if you multiply or divide by a
negative number, you must flip the inequality sign!
• Example: 4x – 2y ≤ 5
- 4x
- 4x
-2y ≤ -4x + 5
Because you
-2
-2 -2
divided by a
negative, you
must flip the ≤
to !
y 2x – 2.5
3, Ab4A
© A Very Good Teacher 2007
Solving Equations and Inequalities, cont…
• Given a function like y = 3x² + 2x – 4 and a
set of independent variables like {-1, 0,
1, 2} and asked to find a corresponding
dependent variable
• Remember that independent variables
represent the x values and dependent
variables represent y values
• Just use the calculator to graph the
function and look at the table to identify
the corresponding y values
3, Ab4A
© A Very Good Teacher 2007
Solving Equations and Inequalities, cont…
• Example: A function is described by the
equation y = 3x² + 2x – 4, in which y is
dependent on x. If a value for the
independent variable is selected from the set
{-1, 0, 1, 2}, which of the following is a
corresponding dependent value?
The answer must be from the y values that correspond to the x values
listed in the question. So, the answer must be one of {-3, -4, 1, 12}.
3, Ab4A
© A Very Good Teacher 2007
Simplifying Expressions
• Use properties to simplify completely
• Example: Which expression is equivalent
to (5t – 4)6t – (5t – 4)(t + 1)?
Multiply to eliminate
30t² - 24t - (5t² +5t - 4t - 4)
parentheses
30t² - 24t – 5t² - 5t + 4t + 4
Combine like terms
25t² -25t + 4
3, Ab4B
© A Very Good Teacher 2007














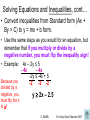












![{ } ] (](http://s1.studyres.com/store/data/008467374_1-19a4b88811576ce8695653a04b45aba9-150x150.png)

