Download N3 Fractions - WIKIMONTESORIENTALES

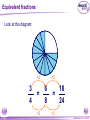
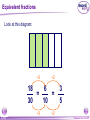
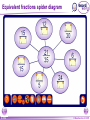
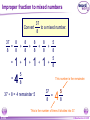
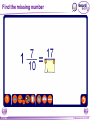
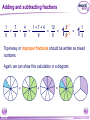
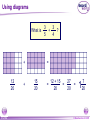
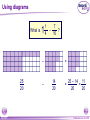
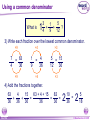
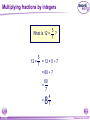
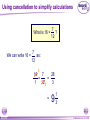
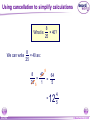
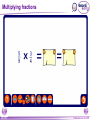
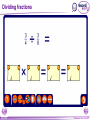
KS4 Mathematics
N3 Fractions
1 of 54
© Boardworks Ltd 2005
Contents
N3 Fractions
N3.1 Equivalent fractions
N3.2 Finding fractions of quantities
N3.3 Comparing and ordering fractions
N3.4 Adding and subtracting fractions
N3.5 Multiplying and dividing fractions
2 of 54
© Boardworks Ltd 2005
Equivalent fractions
Look at this diagram:
×2
3
4
=
×2
3 of 54
×3
6
8
=
18
24
×3
© Boardworks Ltd 2005
Equivalent fractions
Look at this diagram:
×3
2
3
=
×3
4 of 54
×4
6
9
=
24
36
×4
© Boardworks Ltd 2005
Equivalent fractions
Look at this diagram:
÷3
18
30
=
÷3
5 of 54
÷2
6
10
=
3
5
÷2
© Boardworks Ltd 2005
Equivalent fractions spider diagram
6 of 54
© Boardworks Ltd 2005
Cancelling fractions to their lowest terms
A fraction is said to be expressed in its lowest terms if the
numerator and the denominator have no common factors.
Which of these fractions are expressed in their lowest terms?
14
16
7
8
20
27
3
13
15
21
5
7
14
35
2
5
32
15
Fractions which are not shown in their lowest terms can be
simplified by cancelling.
7 of 54
© Boardworks Ltd 2005
Mixed numbers and improper fractions
When the numerator of a fraction is larger than the
denominator it is called an improper fraction.
For example,
15
is an improper fraction.
4
We can write improper fractions as mixed numbers.
15
4
can be shown as
15
=
4
8 of 54
3
3
4
© Boardworks Ltd 2005
Improper fraction to mixed numbers
37
Convert
to a mixed number.
8
37
8
8
8
8
+
+
+
=
8
8
8
8
8
+
1+1+1+1+
5
= 4
8
=
37 ÷ 8 = 4 remainder 5
5
8
5
8
37
=
8
This number is the remainder.
4
5
8
This is the number of times 8 divides into 37.
9 of 54
© Boardworks Ltd 2005
Mixed numbers to improper fractions
2
to a mixed number.
7
3
2
37 =1 + 1 + 1 +
Convert
2
7
7
7
7
2
=
+
+
+
7
7
7
7
23
=
7
To do this in one step,
… and add this number …
3
2
23
=
7
7
… to get the numerator.
Multiply these numbers together …
10 of 54
© Boardworks Ltd 2005
Find the missing number
11 of 54
© Boardworks Ltd 2005
Contents
N3 Fractions
N3.1 Equivalent fractions
N3.2 Finding fractions of quantities
N3.3 Comparing and ordering fractions
N3.4 Adding and subtracting fractions
N3.5 Multiplying and dividing fractions
12 of 54
© Boardworks Ltd 2005
Finding a fraction of an amount
2
What is
of £18?
3
We can see this in a diagram:
2
of £18 = £18 ÷ 3 × 2 = £12
3
13 of 54
© Boardworks Ltd 2005
Finding a fraction of an amount
7
What is
of £20?
10
Let’s look at this in a diagram again:
7
of £20 = £20 ÷ 10 × 7 = £14
10
14 of 54
© Boardworks Ltd 2005
Finding a fraction of an amount
5
What is
of £24?
6
5
1
of £24 =
of £24 × 5
6
6
= £24 ÷ 6 × 5
= £4 × 5
= £20
15 of 54
© Boardworks Ltd 2005
Finding a fraction of an amount
4
What is
of 9 kg?
7
4
To find
of an amount we can multiply by 4 and divide by 7.
7
We could also divide by 7 and then multiply by 4.
4 × 9 kg = 36 kg
36 kg ÷ 7 =
16 of 54
36
7
kg =
5
1
kg
7
© Boardworks Ltd 2005
Finding a fraction of an amount
When we work out a fraction of an amount we
multiply by the numerator
and
divide by the denominator
For example,
2
of 18 litres = 18 litres ÷ 3 × 2
3
= 6 litres × 2
= 12 litres
17 of 54
© Boardworks Ltd 2005
Finding a fraction of an amount
What is
2
of 3.5m?
5
1
To find 1 25 of an amount we need to add 1 times the
amount to two fifths of the amount.
1 × 3.5 m = 3.5 m
so,
18 of 54
1
and
2
of 3.5 m = 1.4 m
5
2
of 3.5 m = 3.5 m + 1.4 m = 4.9 m
5
7
We could also multiply by
5
© Boardworks Ltd 2005
MathsBlox
19 of 54
© Boardworks Ltd 2005
Contents
N3 Fractions
N3.1 Equivalent fractions
N3.2 Finding fractions of quantities
N3.3 Comparing and ordering fractions
N3.4 Adding and subtracting fractions
N3.5 Multiplying and dividing fractions
20 of 54
© Boardworks Ltd 2005
Using decimals to compare fractions
3
7
Which is bigger
or
?
8
20
We can compare two fractions by converting them to
decimals.
3
8
= 3 ÷ 8 = 0.375
7 = 7 ÷ 20 = 0.35
20
0.375 > 0.35
so
21 of 54
3
8
>
7
20
© Boardworks Ltd 2005
Using equivalent fractions
3
5
Which is bigger
or
?
8
12
Another way to compare two fractions is to convert them to
equivalent fractions.
First we need to find the lowest common multiple of 8 and 12.
The lowest common multiple of 8 and 12 is 24.
3
5
Now, write
and
as equivalent fractions over 24.
8
12
×3
3
8
9
=
24
×3
22 of 54
×2
and
5
10
=
12
24
so,
3
8
<
5
12
×2
© Boardworks Ltd 2005
Ordering fractions
23 of 54
© Boardworks Ltd 2005
Mid-points
24 of 54
© Boardworks Ltd 2005
Contents
N3 Fractions
N3.1 Equivalent fractions
N3.2 Finding fractions of quantities
N3.3 Comparing and ordering fractions
N3.4 Adding and subtracting fractions
N3.5 Multiplying and dividing fractions
25 of 54
© Boardworks Ltd 2005
Adding and subtracting fractions
When fractions have the same denominator it is quite easy
to add them together and to subtract them.
For example,
3
5
+
1
5
=
3+1
5
=
4
5
We can show this calculation in a diagram:
+
26 of 54
=
© Boardworks Ltd 2005
Adding and subtracting fractions
7
8
–
3
8
=
7–3
8
=
4
1
8
2
=
1
2
Fractions should always be cancelled down to their lowest
terms.
We can show this calculation in a diagram:
–
27 of 54
=
© Boardworks Ltd 2005
Adding and subtracting fractions
1
7
4
1+7+4
12
+
+
=
=
=
9
9
9
9
9
1
3
9
1
3
=
1
1
3
Top-heavy or improper fractions should be written as mixed
numbers.
Again, we can show this calculation in a diagram:
+
28 of 54
+
=
© Boardworks Ltd 2005
Fractions with common denominators
Fractions are said to have a common denominator if
they have the same denominator.
For example,
11
4
5
,
and
12 12
12
all have a common denominator of 12.
We can add them together:
11
4
5
11 + 4 + 5
20
=
+
+
=
=
12
12
12
12
12
29 of 54
1
8
=
12
1
2
3
© Boardworks Ltd 2005
Fractions with different denominators
Fractions with different denominators are more difficult to add
and subtract.
For example,
What is
5
2
–
?
6
9
We can show this calculation using diagrams:
–
15
18
30 of 54
–
=
4
18
15 – 4
11
=
=
18
18
© Boardworks Ltd 2005
Using diagrams
What is
+
12
20
31 of 54
+
3
3
+
?
5
4
=
15
20
12 + 15
=
=
20
27
20
=
1
7
20
© Boardworks Ltd 2005
Using diagrams
What is
1
1
7
–
?
4
10
–
25
20
32 of 54
–
=
14
20
25 – 14 11
=
=
20
20
© Boardworks Ltd 2005
Using a common denominator
What is
1
3
5
1
+
+
?
4
12
9
1) Write any mixed numbers as improper fractions.
1
3
4
=
7
4
2) Find the lowest common multiple of 4, 9 and 12.
The multiples of 12 are: 12, 24, 36 . . .
36 is the lowest common denominator.
33 of 54
© Boardworks Ltd 2005
Using a common denominator
What is
1
3
5
1
+
+
?
4
12
9
3) Write each fraction over the lowest common denominator.
×9
7
4
= 63
36
×9
×4
1
9
= 4
36
×4
×3
5 = 15
12
36
×3
4) Add the fractions together.
63
4
15
63 + 4 + 15
82
+
+
=
=
=
36
36
36
36
36
34 of 54
2
10
=
36
2
5
18
© Boardworks Ltd 2005
Adding and subtracting fractions
35 of 54
© Boardworks Ltd 2005
Using a calculator
It is also possible to add and subtract fractions using the
abc key on a calculator.
4
For example, to enter 8 we can key in
4
a bc
8
The calculator displays this as:
Pressing the
36 of 54
=
key converts this to:
© Boardworks Ltd 2005
Using a calculator
To calculate:
2
4
+
3
5
using a calculator, we key in:
2
a bc
3
+
4
a bc
5
=
The calculator will display the answer as:
We write this as
37 of 54
1
7
15
© Boardworks Ltd 2005
Fraction cards
38 of 54
© Boardworks Ltd 2005
Contents
N3 Fractions
N3.1 Equivalent fractions
N3.2 Finding fractions of quantities
N3.3 Comparing and ordering fractions
N3.4 Adding and subtracting fractions
N3.5 Multiplying and dividing fractions
39 of 54
© Boardworks Ltd 2005
Multiplying fractions by integers
When we multiply a fraction by an integer we:
multiply by the numerator
and
divide by the denominator
For example,
4
54 ×
= 54 ÷ 9 × 4
9
=6×4
This is
equivalent to
4
of 54.
9
= 24
40 of 54
© Boardworks Ltd 2005
Multiplying fractions by integers
5
What is 12 ×
?
7
5
12 ×
= 12 × 5 ÷ 7
7
= 60 ÷ 7
60
=
7
=
41 of 54
8
4
7
© Boardworks Ltd 2005
Using cancellation to simplify calculations
7
What is 16 ×
?
12
We can write 16 × 7 as:
12
4
16
7
28
×
=
1
12 3
3
=
42 of 54
9
1
3
© Boardworks Ltd 2005
Using cancellation to simplify calculations
8
What is
× 40?
25
8
We can write
× 40 as:
25
8
8
40
64
×
=
25 5
1
5
=
43 of 54
12
4
5
© Boardworks Ltd 2005
Multiplying a fraction by a fraction
3
2
What is
×
?
8
5
To multiply two fractions together, multiply the numerators
together and multiply the denominators together:
3
3
4
12
=
×
8
5
40 10
We could also
cancel at this
step.
44 of 54
3
=
10
© Boardworks Ltd 2005
Multiplying a fraction by a fraction
What is
5
5 12
×
?
6 25
Start by writing the calculation with any mixed numbers as
improper fractions.
To make the calculation easier, cancel any numerators with
any denominators.
7
2
35
14
12
×
=
6 1 25 5
5
=
45 of 54
2
4
5
© Boardworks Ltd 2005
Multiplying fractions
46 of 54
© Boardworks Ltd 2005
Dividing an integer by a fraction
1
What is 4 ÷ ?
3
1
4÷
means, “How many thirds are there in 4?”
3
Here are 4 rectangles:
Let’s divide them into thirds.
1
4÷
= 12
3
47 of 54
© Boardworks Ltd 2005
Dividing an integer by a fraction
2
What is 4 ÷ ?
5
2
4÷
means, “How many two fifths are there in 4?”
5
Here are 4 rectangles:
Let’s divide them into fifths, and count the number of two fifths.
2
4÷
= 10
5
48 of 54
© Boardworks Ltd 2005
Dividing an integer by a fraction
3
What is 6 ÷ ?
4
3
6÷
means, ‘How many three quarters are there in six?’
4
There are 4
1
6÷
= 6 × 4 = 24
quarters in
4
each whole.
So,
3
6÷
= 24 ÷ 3 = 8
4
We can check this by multiplying.
3
8×
=8÷4×3=6
4
49 of 54
© Boardworks Ltd 2005
Dividing a fraction by a fraction
1
1
What is
÷
?
8
2
1
1
÷
means, ‘How many eighths are there in one half?’
8
2
1
Here is of a rectangle:
2
Now, let’s divide the shape into eighths.
1
1
÷
=4
8
2
50 of 54
© Boardworks Ltd 2005
Dividing a fraction by a fraction
4
2
What is
÷
?
5
3
To divide by a fraction we multiply by the denominator and
divide by the numerator.
4
5
2
2
can be written as
÷
×
5
4
3
3
Swap the numerator and
the denominator and
multiply.
This is the reciprocal of
5
10
2
×
=
4
12
3
4
.
5
5
=
6
51 of 54
© Boardworks Ltd 2005
Dividing a fraction by a fraction
What is
Start by writing
3
3
6
3
÷
?
7
5
3 as an improper fraction.
5
3
18
=
5
5
3
3
18
6
18
7
÷
×
=
5
7
5
6 1
21
=
5
1
=
5
4
52 of 54
© Boardworks Ltd 2005
Dividing fractions
53 of 54
© Boardworks Ltd 2005
Multiplying and dividing by fractions
Multiplying and dividing are inverse operations.
When we multiply by a fraction we:
multiply by the numerator
and
divide by the denominator
When we divide by a fraction we:
divide by the numerator
and
multiply by the denominator
54 of 54
© Boardworks Ltd 2005