* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download document
Survey
Document related concepts
Transcript
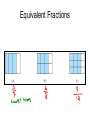
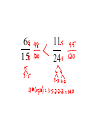
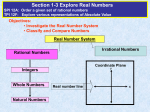
Exploration 5.8 Part 1; #1-7 Part 2; #1-4 Part 3; Choose one of the manipulatives to do #1,3 Part 4; Choose one of the manipulatives to do #1,2 Fractions and Rational Numbers • A rational number is a number whose value can be represented as the quotient or ratio of two integers a and b, where b is nonzero. • A fraction is a number whose value can be expressed as the quotient or ratio of any two numbers a and b, where b is nonzero. • How do rational numbers and fractions differ? Terminology • The number above the horizontal fraction line is called the numerator. • The number below the horizontal fraction line is called the denominator. Contexts for rational numbers • There are 4 contexts or meanings for fractions. • Let’s look at the different contexts in which this rational number has meaning. 3 4 Rational number as a measure • Sylvia grew ¾ of an inch last year. • We have some amount or object that has been divided into b equal amounts, and we are considering a of those amounts. • Keep units. • Diagram: length model • Another example: – 7/20 of my paycheck goes to my car payment. Rational number as a quotient • 4 people want to share 3 candy bars equally. How much candy does each person get? • We have an amount a that needs to be shared or divided equally into b groups. • We should see a per at the end. • In this problem 3/4 candy bar per person tells us how much each person gets. • Diagram: Area model Rational number as operator • ¾ of my shirts are blue. If I have 12 shirts, how many blue shirts do I own? • a/b is a function machine that tells us the extent to which the given object or amount is stretched or shrunk. • If we have 12, ¾ is telling us to take 3 out of every four. • Diagram: Discrete Model. Rational number as a ratio • At a college ¾ of the students are women. • A ratio is a relationship between two quantities. • Diagram: WWWM WWWM … • We can compare parts- women:men=3:1 • We can compare parts to wholewomen:total=3:4 The unit and the whole • Not always the same! • The whole is the given object or amount. The unit is the amount to which we give a value of one. • Tom ate ¾ of a pizza. – Whole is 1 pizza – Unit is 1 pizza • Sylvia grew ¾ of an inch last year. – Whole is ¾ – Unit is 1 in. • 4 people want to share 3 candy bars equally. How much candy does each person get? – Whole is 3 candy bars. – Unit is 1 candy bar. • ¾ of my shirts are blue. If I have 12 shirts, how many blue shirts do I own? – Whole is – Unit is • At a college ¾ of the students are women. – Whole is – Unit is Exploration 5.9 In #1, you are given three rectangles, same size and shape. Use three different ways to divide the rectangles into equal pieces. Work on this in class and finish for Monday. • If the given diagram has a value of 2 ½, show 1. • If the given diagram has a value of ¼, show 1/3. Contexts for fractions • Measure or Part/Whole • Ratio • Operator • Quotient Figure 5.10 Happy Halloween! Equivalency Equi equal - valent value 5 10 2 52 Equivalent Fractions • Fractions are equivalent if they have equal value. Equivalent Fractions Comparing Fractions • Which one is bigger? 3 4 2 3 6 15 11 24 Meanings for fraction: 2/5 • Part-whole: subdivide the whole into 5 equal parts, then consider 2 of the 5 parts. discrete area Length (number line) 0 1/5 2/5 3/5 4/5 1 Meanings for fraction: 2/5 • Ratio: a comparison two quantities. In this case, the first quantity is the number of parts/pieces/things that have a certain quality, and the second quantity is the number of parts/pieces/things that do not share that quality. 2 blue : 3 non-blue 2:3 Or 2 blue : 5 total 2:5 Meanings for fraction: 2/5 • Operator: instead of counting, the operator can be thought of as part of a set, or a stretch/shrink of a given amount. • If the fraction is less than one, then the operator shrinks the given amount. If the fraction is greater than one, then the operator stretches the given amount. • 2/5 of a set might mean take 2 out of every 5 elements of a set. It might also mean 2/5 as large as the original. Meanings for fraction: 2/5 • Quotient: The result of a division. • There are two ways to think about this. • We can think of 2/5 as 2 ÷ 5: I have 2 candy bars to share among 5 people; each person gets 2/5 of the candy bar. If students do not understand this model, then much of algebra will be less meaningful. What is π / 6? How do you solve x/3 = 12? • We can also think of this as the result of a division: I have 16 candy bars to share among 40 people: 16/40 = 2/5. Alexa • We will watch Alexa in just a few moments. Look at her work on page 23 for the second problem. What do you think Alexa was doing in each diagram? • Now pick one. Can this picture be used to mean Part-whole? Ratio? Operator? Quotient? If yes, say why. If no, say why not. • Class Notes pp. 22-23 Now, we’ll watch Alexa • Complete parts 1, 2, and Follow-up Question Part a in your groups. • Now, try Part c (skip b for just a moment). Once you found the value for 5, explain it in words so that someone else will understand. • Now, let’s try part b. Same thing--once you get an answer, try to write it up in words so that someone else will understand. Part d Extra Practice • You have from 10:00 - 11:30 to do a project. At 11, what fraction of time remains? At 11:20, what fraction of time remains? • Use a diagram to explain how you know. Are there certain diagrams that are more effective? Discuss this with your group. Extra Practice • Is 10/13 closer to 1/2 or 1? • Use a diagram to explain how you know. Are there certain diagrams that are more effective? Discuss this with your group. Extra Practice • A teacher asks for examples of fractions that are equivalent to 3/4. One student replied: • How would 1 you respond to 1 2 this answer? 2 • Use a diagram to explain how you know. Are there certain diagrams that are more effective? Discuss this with your group. Alexa’s problem • Children’s thinking p. 22 b. Which contexts can be explained using one of her diagrams? Which ones cannot? Why or why not? Sean’s work • P. 29 not enough room for answers especially for part c. Use the back of the previous page. • P. 33 Language in Mathematics • Sometimes mathematics is called a language. It isn’t really but it has a lot of its own vocabulary, as well as symbols. Because these symbols are used universally across languages, it is sometimes called the “universal language”. Language in Mathematics • Words in math have a precise meaning. • It is important for a teacher to use clear and correct language in talking about math—if the teacher is vague and imprecise, students have great difficulty learning concepts.