Download ENGG2013 Lecture 17

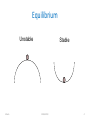
ENGG2013 Unit 17
Diagonalization
Eigenvector and eigenvalue
Mar, 2011.
EXAMPLE 1
kshum
ENGG2013
2
Q6 in midterm
• u(t): unemployment rate in the t-th month.
• e(t)= 1-u(t)
• The unemployment rate in the next month is
given by a matrix multiplication
• Equilibrium: Solve
 Unemployment rate at equilibrium = 0.2
kshum
ENGG2013
3
Equilibrium
Unstable
kshum
Stable
ENGG2013
4
If stable, how fast does it converge
to the equilibrium point?
Slow convergence
0.2
kshum
Fast convergence
0.2
ENGG2013
5
Question
• Suppose that the initial unemployment rate at
the first month is x(1), (for example x(1)=0.25),
and suppose that the unemployment evolves
by matrix multiplication
Find an analytic expression for x(t), for all t.
kshum
ENGG2013
6
EXAMPLE 2
kshum
ENGG2013
7
How to count?
• Count the number of binary strings of length n
with no consecutive ones.
kshum
ENGG2013
8
SOLVING RECURRENCE RELATION
kshum
ENGG2013
9
•
•
•
•
F1 = 1
F2 = 1
For n > 2, Fn = Fn-1+Fn-2.
The Fibonacci numbers are
– 1,1,3,5,8,13,21,34,55,89,144
kshum
ENGG2013
http://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci numbers
10
A matrix formulation
• Define a vector
• Initial vector
• Find the recurrence relation in matrix form
kshum
ENGG2013
11
A general question
• Given initial condition
and for t  2
Find v(t) for all t.
kshum
ENGG2013
12
Matrix power
• Need to raise a matrix to a very high power
kshum
ENGG2013
13
A trivial special case
• Diagonal matrix
• The solution is easy to find
• Raising a diagonal matrix to the power t is
easy.
kshum
ENGG2013
14
Decoupled equations
• When the equation is diagonal, we have two
separate equation, each in one variable
kshum
ENGG2013
15
DIAGONALIZATION
kshum
ENGG2013
16
Problem reduction
• A square matrix M is called diagonalizable if
we can find an invertible matrix, say P, such
that the product P–1 M P is a diagonal matrix.
• A diagonalizable matrix can be raised to a high
power easily.
– Suppose that P–1 M P = D, D diagonal.
– M = P D P–1.
– Mn = (P D P–1) (P D P–1) (P D P–1) … (P D P–1)
= P Dn P–1.
kshum
ENGG2013
17
Example of diagonalizable matrix
• Let
• A is diagonalizable because we can find a
matrix
such that
kshum
ENGG2013
18
Now we know how fast it
converges to 0.2
• The matrix can be diagonalized
kshum
ENGG2013
19
Convergence to equilibrium
• The trajectory of the unemployment rate
– the initial point is set to 0.1
0.2
0.19
0.18
Unemployment rate
0.17
0.16
0.15
0.14
0.13
0.12
0.11
0.1
kshum
1
2
3
4
5
6
month (t)
ENGG2013
7
8
9
10
20
EIGENVECTOR AND EIGENVALUE
kshum
ENGG2013
21
How to diagonalize?
• How to determine whether a matrix M is
diagonalizable?
• How to find a matrix P which diagonalizes a
matrix M?
kshum
ENGG2013
22
From diagonalization to
eigenvector
• By definition a matrix M is diagonalizable if
P–1 M P = D
for some invertible matrix P, and diagonal
matrix D.
or equivalently,
kshum
ENGG2013
23
The columns of P are special
• Suppose that
kshum
ENGG2013
24
Definition
• Given a square matrix A, a non-zero vector v is
called an eigenvector of A, if we an find a real
number  (which may be zero), such that
Matrix-vector product
Scalar product of a vector
• This number  is called an eigenvalue of A,
corresponding to the eigenvector v.
kshum
ENGG2013
25
Important notes
• If v is an eigenvector of A with eigenvalue ,
then any non-zero scalar multiple of v also
satisfies the definition of eigenvector.
k0
kshum
ENGG2013
26
Geometric meaning
• A linear transformation L(x,y) given by: L(x,y) = (x+2y, 3x-4y)
x  x + 2y
y  3x – 4y
• If the input is x=1, y=2 for example,
the output is x = 5, y = -5.
kshum
27
Invariant direction
• An Eigenvector points at a direction which is invariant under the linear
transformation induced by the matrix.
• The eigenvalue is interpreted as the magnification factor.
• L(x,y) = (x+2y, 3x-4y)
• If input is (2,1), output is magnified by a factor of 2, i.e., the eigenvalue is 2.
kshum
28
Another invariant direction
•
•
L(x,y) = (x+2y, 3x-4y)
If input is (-1/3,1), output is (5/3,-5). The length is increased by a factor of 5, and
the direction is reversed. The corresponding eigenvalue is -5.
kshum
29
Eigenvalue and eigenvector of
First eigenvalue = 2, with eigenvector
where k is any nonzero real number.
Second eigenvalue = -5, with eigenvector
where k is any nonzero real number.
kshum
ENGG2013
30
Summary
• Motivation: want to solve recurrence
relations.
• Formulation using matrix multiplication
• Need to raise a matrix to an arbitrary power
• Raising a matrix to some power can be easily
done if the matrix is diagonalizable.
• Diagonalization can be done by eigenvalue
and eigenvector.
kshum
ENGG2013
31