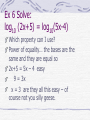Download 11.4 Logarithmic Functions

Warm-Up 4/30
The Park family is saving for their son's education. If they deposit
$31,500 in an account earning 7.6%, compounded continuously, how
much will be in the account when Sam goes to college in 9 years?
What if it is compounded annually?
Answer: $62,426.36
$60,900.52
11.4 Logarithmic Functions
bx
y
x
=
b
The inverse of y =
is _______
logarithm
The function x = by is called a___________
y = logbx
It is usually written ______________
Read “ y equals log base b of x”
 Logarithmic functions are the inverse of
exponential functions
Definition:
y= logbx if and only if x=by
“b” can’t be 1 and it must be positive
EX1: Write in exponential form
a) log273 = 1/3
Answers:
1
3
27  3
b) log164 = ½
1
2
16  4
EX2: Write each equation in logarithmic form
a) 210 = 1024
b) 2-3 = 1/8
Answers: log2 1024 = 10
b) log2 1/8 = -3
Ex3 Evaluate: log51/625
This is a number, its an operation
The answer to a log will be an exponent
Think 5 to the what power is 1/625
Since it is a fraction the exponent will
be negative
5 4 = 625 so 5 –4 =1/625
So log51/625 = -4
Ex 4: evaluate log432
Think 4 to the what equals 32
Nothing – dang it
Re-write: 4x = 32
Get the bases the same: (22)x = 25
Bases are same so just set exponents
equal to each other
2x = 5
X = 2.5
Since a log is inverse of an exponent it follows
the exponent rules…
m and n are positive numbers, b is a positive number other
than 1 and p is any real number…
Product
Definition
logbmn =logbm +logbn
Quotient
logbm/n = logbm – logbn
Power
logbmp = p(logbm)
Power of
equality
If logbm=logbn then m=n
Property
Ex 6 Solve:
log10 (2x+5) = log10(5x-4)
Which property can I use?
Power of equality… the bases are the
same and they are equal so
2x+5 = 5x – 4 easy
9 = 3x
x = 3 are they all this easy – of
course not you silly geese.
Ex 7: Solve log3(4x+5) – log3(3 – 2x) = 2
Don’t have logs on both sides so we can’t use
the equality property.
Always try to simplify – subtraction, write it as
a quotient log 4 x  5  2
3
3  2x
Re-write using definition of logs 32  4 x  5
3  2x
now solve /cross multiply
9(3  2 x)  4 x  5
27 – 18x = 4x + 5
-22x=-22
x=1
Ex8: log3(x+2)+log3(x-6) = 2
Write as a single log:
Use log properties:
log3(x+2)(x – 6)=2
No logs on both sides
Write in exponential form
32 = (x+2)(x – 6)
Solve:
9 = x2 – 4x – 12
0 = x2 – 4x – 21
This is a Quadratic
You should know how to solve (x – 7)(x + 3)=0
CHECK in original equation
x = 7 x = -3
You might need to eliminate an answer
Can’t take the log of a neg #
Ex 9: ½ log8(x+1) – ½ log825 = log84
Use your properties to write as a single log
on each side
x 1
log8
 log8 4
1/2
25
x 1
4
5
x  1  20
Subtraction means division
Cross multiply and solve
Square both sides
x  1  400
x  399
Summary:
Homework: pg 723 # 20-52