Download Base e and Natural Logarithms 10.5

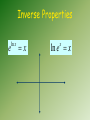
Base e and
Natural Logarithms
E.Q: How do I use logarithms to solve exponential
equations?
How do I use the properties of exponents to
simplify logarithmic expressions and solve
logarithmic equation?
CCSS: F.IF.7e; F.LE.3; F.IF.5; F.BF.5
CCSS: F.IF.7e; F.IL.3
•
GRAPH exponential and logarithmic functions,
showing intercepts and end behavior.
• OBSERVE using graphs and tables that a quantity
increasing exponentially eventually EXCEEDS a
quantity increasing linearly, quadratically, or (more
generally) as a polynomial function.
CCSS: F.IF.5; F.BF.5
• RELATE the domain of a function to its graph and,
where applicable, to the quantitative relationship it
describes. For example, if the function h(n) gives the
number of person-hours it takes to assemble n
engines in a factory, then the positive integers would
be an appropriate domain for the function.*
Emphasize the selection of a model function based on
behavior of data and context
•
Understand the inverse relationship between
exponents and logarithms and use this relationship to
solve problems involving logarithms and exponents.
Standards for Mathematical Practice
1. Make sense of problems and persevere in solving
them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the
reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated
reasoning.
History
The number e is a famous
irrational number, and is one of
the most important numbers in
mathematics. The first few digits
are
2.7182818284590452353602874713527...
It is often called Euler's number
after Leonhard Euler. e is the
base of the natural logarithms
(invented by John Napier).
Calculating
The value of (1 + 1/n)n approaches e as n
gets bigger and bigger:
(1 + 1/n)n
n
1
2.00000
2
2.25000
5
2.48832
10
2.59374
100
2.70481
1,000
2.71692
10,000
2.71815
100,000
2.71827
Vocabulary
natural base: the number e, which is found using
 1
1  
 n
n
• the base rate of growth shared by all continually
growing processes
• Used heavily in science to model quantities that grow
& decay continuously
natural base exponential function: an exponential
function with base e
Vocabulary
natural logarithm: a logarithm with base e
The natural log gives you the time needed
to reach a certain level of growth.
natural logarithmic function: the inverse
of the natural base exponential function
Ex 1
e
0.5
Use a calculator to estimate
to four decimal places.
Ex 2
e
8
Ex 3
Ex 4
ln 3
1
ln
4
Writing Equivalent Expressions
Exponential logarithmic
Write an equivalent equation in the other form.
Ex 5
Ex 6
e x  23
e 6
x
Ex 7
Ex 8
ln x  1.2528
ln x  2.25
Inverse Properties
e
ln x
x
ln e  x
x
Writing Equivalent Expressions
Ex 9
Evaluate
Ex 10
e
ln 21
Ex 11
Evaluate
ln e
x2 1
Evaluate
e
ln  x 3
Ex 12
Evaluate
ln e
7
Solving Equations
Ex 13
Solve the following equations.
3e2 x  4  10
Ex 14
2 x
2e  5  15
Solving Equations
Ex 15
Solve the following equations.
ln 3x  0.5
Ex 16
ln  x  3  3