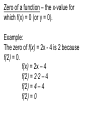Download Unit 1 - Typepad

Unit 2
Algebra Investigations
Vocabulary
Monomial - a number, a variable or
the product of a number and one or
more variables with the whole
number exponents. This type of
polynomial has only one term.
Examples:
1, -101,
X, Y, 2X, X7
-3XY, AB5, or C2D2
Binomial – is a polynomial with
two terms. “Think of bicycle
which has 2 wheels”
Examples:
2X -1
-3Y + 3
-5X2 + 10X
Trinomial is a polynomial with three
terms. “Think of a tricycle which
has 3 wheels”
Examples:
5XY + 4Y – 7
X2 + 4X + 2
AB3 – AB2 + AB
Polynomial – is a monomial or a sum of
monomials (binomial, trinomial or the
sum of more than three terms). We
normally think of it as having 4 or more
terms.
Examples:
X3 + 4X2 – 7x + 1
-YZ2 + YZ + Y - 6
Leading coefficient – when a polynomial
is written so that the exponents of a
variable decrease from left to right, the
coefficient of the first term is called the
leading coefficient.
Examples:
3X3 + 4X2 – 7x + 1
Leading coefficient is 3
-5YZ2 + YZ + Y - 6
Leading coefficient is -5
Like terms – two terms are like terms if all
parts of both terms except the numerical
coefficients are the same.
Examples:
3X3, 4X3, -5X3, ½X3, ¾X3
Variables and Exponents in red are the same, but
the leading coefficients in blue are all different.
–7x, 5x, -x, x, ½x, ¾x
Exponents in these terms are all 1 (we don’t
usually write them down), but the leading
coefficients in red are all different.
1, 2, ¾, -3, 5, -½ All are numbers, exponents are
all 0.
Degree of a polynomial – Put the
polynomial in standard form and
then determine which of exponents
of the variables is the largest . The
degree of a nonzero constant term
(a number like 1, -9, 101) is 0.
Examples:
X3 + 4X2 – 7x + 1
Degree is 3
-YZ2 + YZ + Y – 6 Degree is 2
Degree of a monomial–determine the
degree of the term. The number like
1, -9, 101) is 0.
Examples:
X3
Degree is 3
4X2
Degree is 2
– 7x
Degree is 1
5
Degree is 0
Standard form of a polynomial –
means to write the polynomial so
that the exponents decrease from
left to right (numerical order).
(numbers should always be last).
Example:
12 + 9X3 + 5X6 – 3X4 - 5X
Standard form would be:
5X6 – 3X4 + 9X3 - 5X + 12
Binomial Theorem and Pascal’s
Triangle can be used to find the
coefficients in a binomial expansion (a +
b)n where n is a positive integer.
Example:
binomial expansion
(X + 1)2
1
(X + 1)(X + 1)
1 1
1X2 + 2X + 1
1 2 1
Pascal’s triangle
FOIL is a method for expanding
product of two binomials (x+1)(x+1).
First
Outer
Inner
Last
multiply the first terms in
each binomial
multiply the outer terms in
each binomial
multiply the inner
terms of each binomial
multiply the last terms of
each binomial
Factor – a factor is one of two or more
expressions that are multiplied together
to form a more complicated expression.
Examples:
algebraic expression
2X2 + 2X
factors
=
2X ∙ (X + 1)
factors
X2 - 2X – 15
= (X + 3) ∙ (X – 5)
Factoring – the process or splitting a
complicated expression into product of
two or more simpler expressions
(factors).
Example:
algebraic expression
2X2 + 2X
X2 - 2X – 15
factored form
=
2X(X + 1)
= (X + 3)(X – 5)
Zero of a function – the x-value for
which f(x) = 0 (or y = 0).
Example:
The zero of f(x) = 2x - 4 is 2 because
f(2) = 0.
f(x) = 2x – 4
f(2) = 2∙2 – 4
f(2) = 4 – 4
f(2) = 0
Factor completely-A factorable
polynomial with integer coefficients is
factored completely if it is written as
a product of unfactorable
polynomials with integer coefficients.
Factor by grouping-To factor a
polynomial with four terms by
grouping, factor a common
monomial from pairs of terms,
and then look for a common
binomial factor.
Simplest form-An expression
whose numerator and
denominator have no factors in
common other than 1.
Extraneous solution – a solution of a
transformed equation that is not a
solution of the original equation.
Example:
6 x  x
6  x  x2
x2  x  6  0
( x  3)( x  2)  0
x  3
x2
x = 2 is a solution but x = -3 does not
satisfy the original equation.
Asymptote – A line that the graph
approaches more and more
closely.
Radical expression – An
expresssion that contains a
radical, such as a square root,
cube root or other root.
Example:
Radical equation- An equation
that contains a radical expression
with a variable in the radicand.
Examples:
2 x 8  0
3x  17  x  21
Radical conjugates- The
expressions a + √b and a - √b
where a and b are rational
numbers (the only difference
between them is the sign)
Example:
7 2
7 2
Rationalizing the denominatorthe process of eliminating radical
from an expression’s
denominator by multiplying the
expression by an appropriate
form of 1.
The product property of radicals
states that the square root of a
product equals the product of the
square roots of the factors.
Example:
ab  a  b
The quotient property of radicals
states that the square root of a
quotient equals the quotient of the
square roots of the numerators and
denominators.
Example:
a
a

b
b
Where
a0
b0
Rational function-A function
whose rule is given by a fraction
whose numerator and
denominator are polynomials and
whose denominator is not 0.
Examples:
1
y
x
2x 1
y
x 1
Rational expression-An
expression that can be written as
a ratio of two polynomials where
the denominator is not 0.
Examples:
5
x 1
x 8
10 x
Excluded value- A number that
makes a rational expression
undefined.
Example:
3 is an excluded value of the
expression
2
x3
because 3 makes the value of the
denominator 0.
Simplest form of a radical expressionA radical expression that has no
perfect square factors other than 1 in
the radicand, no fractions in the
radicand, and no radicals appearing in
te denominator of a fraction.
Example:
32  2 16  4 2
Simplest form of a rational
expression- A rational expression
whose numerator and denominator
have no factors in common other than
1.
Example:
2x
2

x( x  3) x  3
Area model for polynomial
arithmetic – is a way to visually
represent multiplying two
polynomials using geometry.
Coefficient-A coefficient is a
technical term for something that
multiplies something else
(usually applied to a constant
multiplying a variable). In the
quadratic equation
Ax 2  Bxy  Cy 2  Dx  Ey  F  0
A, B, C, D and E are the coefficients
Term-A term is part of a sum. The
different terms in the expression is
separated by addition/subtraction
signs.
Ax  Bxy  Cy  Dx  Ey  F  0
2
2
2
2
Ax , Bxy, Cy , Dx, Ey, F
Are the terms of the sum.