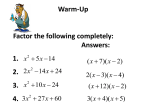Download Chapter 5

7.1 The Greatest Common Factor
and Factoring by Grouping
•
Finding the Greatest Common Factor:
1. Factor – write each number in factored form.
2. List common factors
3. Choose the smallest exponents – for variables
and prime factors
4. Multiply the primes and variables from step 3
•
Always factor out the GCF first when
factoring an expression
7.1 The Greatest Common Factor
and Factoring by Grouping
•
Example: factor 5x2y + 25xy2z
5x y  5 x y z
2
1
2 1 0
25 xy z  5 x y z
2
2 1 2 1
GCF  5 x y z  5 xy
1 1 1 0
5 x y  25 xy z  5 xy( x  5 yz )
2
2
7.1 The Greatest Common Factor
and Factoring by Grouping
•
Factoring by grouping
1. Group Terms – collect the terms in 2 groups
that have a common factor
2. Factor within groups
3. Factor the entire polynomial – factor out a
common binomial factor from step 2
4. If necessary rearrange terms – if step 3 didn’t
work, repeat steps 2 & 3 until you get 2
binomial factors
7.1 The Greatest Common Factor
and Factoring by Grouping
• Example:
10 x 2  12 y 2  15xy  8 xy
 2(5 x 2  6 y 2 )  xy(15  8)
This arrangement doesn’t work.
• Rearrange and try again
10 x 2  15 xy  12 y 2  8 xy
 5 x(2 x  3 y )  4 y (3 y  2 x)
 (5 x  4 y )( 2 x  3 y )
7.2 Factoring Trinomials of the Form
2
x
•
+ bx + c
Factoring x2 + bx + c (no “ax2” term yet)
Find 2 integers: product is c and sum is b
1. Both integers are positive if b and c are
positive
2. Both integers are negative if c is positive and
b is negative
3. One integer is positive and one is negative if c
is negative
7.2 Factoring Trinomials of the Form
2
x
+ bx + c
• Example: x 2  5 x  4
4  1  5; 4  1  4
( x  4)( x  1)
• Example: x 2  4 x  21
7  3  4; 7  (3)  21
( x  7)( x  3)
7.3 Factoring Trinomials of the Form
2
ax + bx + c
•
Factoring ax2 + bx + c by grouping
1. Multiply a times c
2. Find a factorization of the number from step 1
that also adds up to b
3. Split bx into these two factors multiplied by x
4. Factor by grouping (always works)
7.3 Factoring Trinomials of the Form
2
ax + bx + c
• Example:
8 x 2  14 x  15
ac  120  60  ( 2)  30  (4)
 15  (8)  20  ( 6)
b  14  20  6
• Split up and factor by grouping
8 x 2  14 x  15  8 x 2  20 x  6 x  15
 4 x( 2 x  5)  3( 2 x  5)
 (4 x  3)( 2 x  5)
7.3 Factoring Trinomials of the Form
2
ax + bx + c
•
Factoring ax2 + bx + c by using FOIL (in
reverse)
1. The first terms must give a product of ax2
(pick two)
2. The last terms must have a product of c (pick
two)
3. Check to see if the sum of the outer and inner
products equals bx
4. Repeat steps 1-3 until step 3 gives a sum = bx
7.3 Factoring Trinomials of the Form
2
ax + bx + c
• Example:
2 x  7 x  6  (2 x  ?)( x  ?)
2
try (2 x  1)( x  6)  2 x  13 x  6 incorrect
2
try (2 x  6)( x  1)  2 x 2  8 x  6 incorrect
try (2 x  3)( x  2)  2 x 2  7 x  6 correct
7.3 Factoring Trinomials of the Form
2
ax + bx + c
• Box Method (not in book):
2 x 2  7 x  6  (2 x  ?)( x  ?)
2x ?
x 2x2
?
6
7.3 Factoring Trinomials of the Form
2
ax + bx + c
• Box Method – keep guessing until crossproduct terms add up to the middle value
2x 3
2
x 2 x 3x
2 4x 6
so 2 x 2  7 x  6  (2 x  3)( x  2)
7.4 Factoring Binomials and Perfect
Square Trinomials
• Difference of 2 squares:
x 2  y 2  x  y   x  y 
• Example:
9  w2  32  w2  3  w 3  w
• Note: the sum of 2 squares (x2 + y2) cannot
be factored.
7.4 Factoring Binomials and Perfect
Square Trinomials
• Perfect square trinomials:
x  2 xy  y   x  y 
2
2
2
x  2 xy  y   x  y 
2
2
2
• Examples:
2
2
2
2
m  6m  9  m  23m   3  m  3
25 z  10 z  1  5 z   25 z   1  5 z  1
2
2
2
2
7.4 Factoring Binomials and Perfect
Square Trinomials
• Difference of 2 cubes:

x  y  x  y  x  xy  y
3
3
• Example:
2

2

w  27  w  3  w  3 w  3w  9)
3
3
3
2

7.4 Factoring Binomials and Perfect
Square Trinomials
• Sum of 2 cubes:

x  y  x  y  x  xy  y
3
3
• Example:
2

2

w  27  w  3  w  3 w  3w  9)
3
3
3
2

7.4 Factoring Binomials and Perfect
Square Trinomials
•
Summary of Factoring
1. Factor out the greatest common factor
2. Count the terms:
– 4 terms: try to factor by grouping
– 3 terms: check for perfect square trinomial. If not
a perfect square, use general factoring methods
– 2 terms: check for difference of 2 squares,
difference of 2 cubes, or sum of 2 cubes
3. Can any factors be factored further?
7.5 Solving Quadratic Equations
by Factoring
• Quadratic Equation:
ax 2  bx  c  0
• Zero-Factor Property:
If a and b are real numbers and if ab=0
then either a = 0 or b = 0
7.5 Solving Quadratic Equations
by Factoring
•
Solving a Quadratic Equation by factoring
1. Write in standard form – all terms on one side
of equal sign and zero on the other
2. Factor (completely)
3. Set all factors equal to zero and solve the
resulting equations
4. (if time available) check your answers in the
original equation
7.5 Solving Quadratic Equations
by Factoring
• Example:
2x  5  7x
2
standard form : 2 x  7 x  5  0
2
factored : (2 x  5)( x  1)  0
2 x  5  0 or x  1  0
solutions : x  2.5, x  1
7.6 Applications of Quadratic
Equations
• This section covers applications in which
quadratic formulas arise.
Example: Pythagorean theorem for right
triangles (see next slide)
2
2
2
a b  c
7.6 Applications of Quadratic
Equations
• Pythagorean Theorem: In a right triangle, with the
hypotenuse of length c and legs of lengths a and b,
it follows that c2 = a2 + b2
c
a
b
7.6 Applications of Quadratic
Equations
• Example
x
( x  1)  x  ( x  2)
2
2
2
x2  2x 1 x2  x2  4x  4
x  2x  3  0
( x  3)( x  1)  0
x3
2
x+2
x+1
9.3 Linear Inequalities in
Two Variables
• A linear inequality in two variables can be
written as:
Ax  By  C or Ax  By  C or
Ax  By  C or Ax  By  C
where A, B, and C are real numbers and
A and B are not zero
9.3 Linear Inequalities in
Two Variables
•
Graphing a linear inequality:
1. Draw the graph of the boundary line.
Make it solid for  or 
Make it dashed for  or 
2. Choose a test point that is not on the line.
3. If the test point satisfies the inequality, shade
the side it is on, otherwise shade the opposite
side.
9.4 Systems of Linear Equations in
Three Variables
• Linear system of equation in 3 variables:
Ax  By  Cz  D
Ex  Fy  Gz  H
Ix  Jy  Kz  L
• Example:
4x  8 y  z  2
x  7 y  3z  14
2x  3y  2z  3
9.4 Systems of Linear Equations in
Three Variables
•
Graphs of linear systems in 3 variables:
1. Single point (3 planes intersect at a point)
2. Line (3 planes intersect at a line)
3. No solution (all 3 equations are parallel
planes)
4. Plane (all 3 equations are the same plane)
9.4 Systems of Linear Equations in
Three Variables
•
Solving linear systems in 3 variables:
1. Eliminate a variable using any 2 equations
2. Eliminate the same variable using 2 other
equations
3. Eliminate a different variable from the
equations obtained from (1) and (2)
9.4 Systems of Linear Equations in
Three Variables
•
Solving linear systems in 3 variables:
4. Use the solution from (3) to substitute into 2
of the equations. Eliminate one variable to
find a second value.
5. Use the values of the 2 variables to find the
value of the third variable.
6. Check the solution in all original equations.