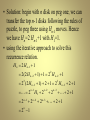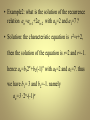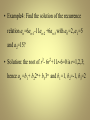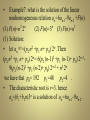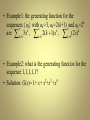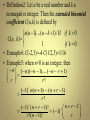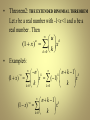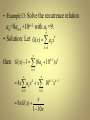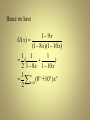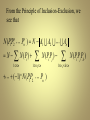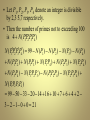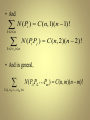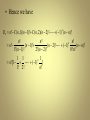* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download A n
List of first-order theories wikipedia , lookup
Collatz conjecture wikipedia , lookup
History of the function concept wikipedia , lookup
Non-standard calculus wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Elementary mathematics wikipedia , lookup
System of linear equations wikipedia , lookup
Chapter 7 Advance Counting
Techniques
Content
Recurrence relations
Generating function
The principle of inclusion-exclusion
Recurrence relations
• Definition: a recurrence relation for the sequence
{an} is an equation that express an in terms of the
sequence , namely a1 , a2, …, an-1 , for all integers n
with n>n0. where n0 is a nonnegative integer. A
sequence is called a solution of a recurrence relation
if its term satisfy the recurrence relation.
• The initial conditions for a sequence specify the
terms that precede the first term where the
recurrence relation takes effect.
• Example1: let {an} be a sequence that satisfies
the recurrence relation an= an-1- an-2 for
n=2,3,4,… and suppose that a0=3 and a1=5.
what are a2 and a3?
• Example2: determine whether the sequence {an}
is a solution of the recurrence relation
an= 2an-1- an-2 for n=2,3,4,….
(1) an= 3n
(2) an= 2n
(3) an= 5
Modeling with recurrence relation
• Example3: Compound Interest
Suppose that a person depots $10000 in a saving
account at a bank yielding 11% per year with
interest compound annually. How much will be in
the account after 30 years?
• Solution: Pn=Pn-1+0.11Pn-1=1.11Pn-1
using a iterative approach to find a formula Pn .
Pn=(1.11)nP0= (1.11)3010000=$228922.97
• Example4: Rabbits and the Fibonacci Numbers
A young pair of rabbits (one of each sex) is placed
on an island. A pair of rabbits does not breed until
they are 2 months old. After they are 2 months old,
each pair of rabbits produces another pair each
month. Find a recurrence relation for the number of
pairs of rabbits on the island after n months,
assuming that no rabbits ever die.
• Solution: fn=fn-1+fn-2 with f1=1 and f2=1.
• Example5: The Tower of Hanoi
The Hanoi Tower consists of three pegs mounted on
a board together with disks of different sizes.
Initially these disks are placed on the first peg in
order of size, with the largest on the bottom. The
rule of the puzzle allow disks to be moved one at a
time from one peg to another as long as a disk is
never placed on top of a smaller disk. The goal of
the puzzle is to have all the disks on the second peg
in order of size, with the largest on the bottom. Let
Hn denote the number of moves needed to solve the
Tower of Hanoi problem with n disks. Set up a
recurrence relation for the sequence {Hn}.
• Solution: begin with n disk on peg one, we can
transfer the top n-1 disks following the rules of
puzzle, to peg three using Hn-1 moves. Hence
we have Hn=2 Hn-1+1 with H1=1.
• using the iterative approach to solve this
recurrence relation.
H n 2 H n1 1
2(2 H n2 1) 1 2 2 H n2 1
22 (2 H n3 1) 2 1 23 H n3 2 1
2n1 H1 2n2 2n3
2n1 2 n2 2 n3
2n 1
2 1
2 1
• Example6: Find a recurrence relation and give
initial conditions for the number of bit strings of
length n that do not have two consecutive 0s.
How many such bit strings are there of length
five?
• Solution: let an denote the number of bit strings
of length n that do not have two consecutive 0s.
To obtain a recurrence relation for {an}, note
that by the sum rule, the number of bit strings
of length n that do not have two consecutive 0s
equals the number of such bit strings ending
with a 0 plus the number of such bit strings
ending with a 1.
End with a 1
Any bit string of length n-1 with
no two consecutive 0s
End with a 0
Any bit string of length n-2 with
no two consecutive 0s
1
1 0
an1
an2
We will assume that n 3 , so that the bit string has at
least 3 bits.
Hence we have an=an-1+an-2 for n 3 with a1=2.
• Example7: Codeword Enumeration
A computer system consider a string of decimal
digits a valid codeword if it contains an even
number of 0 digits. For instance, 1230407869 is
valid, whereas 120987045608 is not valid. Let
an be the number of valid n-digit codeword.
Find a recurrence relation for an.
•
Solution: There are two ways to construct a valid
string with n digits from a string with one fewer
digit.
(1) A valid string of n-digits can be obtained by
appending a valid string of n-1 digits with a digit
other than 0. namely 9an-1 ways there are.
(2) A valid string of n-digits can be obtained by
appending a 0 to a string of length n-1 that is not
valid. Then there are 10n-1-an-1.
Hence an= 9an-1+ 10n-1-an-1= 8an-1+ 10n-1 with a1=9.
Solving Recurrence Relations-1
•
•
Definition1 : A linear homogeneous recurrence
relation of degree k with constant coefficients is
a recurrence relation of the form
an c1an1 c2an2 ck ank
where c1 , c2 , , ck are real numbers, and ck 0 .
Example1: (1) Pn=Pn-1+0.11Pn-1=1.11Pn-1
(2) fn=fn-1+fn-2 with f1=1 and f2=1.
(3) Hn=2 Hn-1+1 with H1=1
• Characteristic equation and characteristic roots
Definition2: assume that a recurrence relation is
an c1an1 c2an2
ck ank
then the equation
r k c1r k 1 c2r k 2 ck 1r ck 0
is called characteristic equation ; and the solution of
the equation are called characteristic roots.
• Theorem1: Let c1 and c2 be real numbers.
Suppose that r2-c1r-c2=0 has two distinct roots
r1 and r2. then the sequence {an} is a solution
of the recurrence relation an=c1an-1+c2an-2 if
and only if an 1r1n 2 r2n for n=0,1,2,…
where 1 , 2 are constants and are determined
by the initial conditions.
• Example2: what is the solution of the recurrence
relation an=an-1+2an-2 with a0=2 and a1=7 ?
• Solution: the characteristic equation is r2=r+2,
then the solution of the equation is r=2 and r=-1.
hence an=b12n+b2(-1)n with a0=2 and a1=7. thus
we have b1= 3 and b2=-1. namely
an=3 . 2n-(-1)n
• Theorem2: Let c1 and c2 be real numbers with
c20, Suppose that r2- c1r- c2=0 has only one
root r0. then a sequence {an} is a solution of
the recurrence relation an=c1an-1+c2an-2 if and
only if an 1r0n 2 nr0n for n=0,1,2,…
where 1 , 2 are constants and are determined
by the initial conditions.
• Example3: what is the solution of the recurrence
relation an=6an-1-9an-2 with a0=1 and a1=6?
• Solution: the root of r2- 6r+9=0 is r=3 , hence
an=b13n+b2 n3n with a0=1 and a1=6.
an=3n+n3n with a0=1 and a1=6.
• Theorem3: Let c1 , c2 ,…, ck be real numbers .
Suppose that rk- c1rk-1 -…-r- ck=0 has k distinct
root r1, r2, …, rk. Then a sequence {an} is a
solution of the recurrence relation
an=c1an-1+c2an-2 +…+ ckan-k
if and only if an =b1r1n+ b2r2n+ …+ bkrkn
for n=0,1,2,… , where b1, … , bk are constants
and are determined by the initial conditions.
• Example4: Find the solution of the recurrence
relation an=6an-1-11an-2 +6an-3 with a0=2, a1=5
and a2=15?
• Solution: the root of r3- 6r2+11r-6=0 is r=1,2,3;
hence an =b1+ b22n+ b33n and b1=1, b2=-1, b3=2
• Theorem4: Let c1 , c2 ,…, ck be real numbers .
Suppose that rk- c1rk-1 -…-r- ck=0 has t distinct root
r1, r2, …, rt with multiplicities m1, m2,…, mt and
m1+m2+…+mt =k. Then a sequence {an} is a solution
of the recurrence relation
an=c1an-1+c2an-2 +…+ ckan-k
if and only if an =(b10+ b11 n+…+ b1m1-1 nm1-1 )r1n+
+ …+ (bt0+ bt1 n+…+ btmt-1 nmt-1 ) rtn
for
n=0,1,2,… , where bij are constants and are
determined by the initial conditions.
• Example5: what is the solution of the recurrence
relation an=-3an-1-3an-2 -an-3 with a0=1, a1=-2 and
a2=-1?
• Solution: the root of r3+3r2+3r+1=0 is r=-1of
multiplicity three;
hence an =(b1+ b2n+ b3n2 )(-1)n
and b1=1, b2=3, b3=-2
Linear Nonhomogeneous Recurrence
Relations with Constant Coefficients
• Definition: the recurrence relation
an=c1an-1+c2an-2 +…+ ckan-k +F(n)
is called Linear Nonhomogeneous Recurrence
Relations with Constant Coefficients.
• an=c1an-1+c2an-2 +…+ ckan-k is called the
associated homogeneous recurrence relation.
• Theorem5: If {an (p)} is a particular solution of the
nonhomogeneous linear recurrence relation with
constant coefficients
an=c1an-1+c2an-2 +…+ ckan-k +F(n) ,
Then every solution is of the form {an (p) + an (h) } ,
where {an (h) } is a solution of the recurrence
relation of the associated homogeneous recurrence
relation
an=c1an-1+c2an-2 +…+ ckan-k .
• Example6: what is the solution of the recurrence
relation an=5an-1-6an-2 +7n with a0=2, a1=5 ?
• Solution: the solution of an=5an-1-6an-2 is
an (h) =b13n+b22n , since F(n)=7n,
assume that an (p) =c 7n , where c is a constant.
Hence c 7n =5 c 7n-1 -6 c 7n-2 + 7n , we have
c =49/20, namely that an (p) =(49/20) 7n . Then
we can determine the coefficients b1 and b2 .
• Theorem6: If {an} satisfies the nonhomogeneous
linear recurrence relation with constant coefficients
an=c1an-1+c2an-2 +…+ ckan-k +F(n)
where c1, c2,…, ck are real numbers and
F(n) =(bt nt+ bt-1nt-1 +…+ b1n+b0) sn
where b0, b1, … , bt and s are real numbers.
(1) If s is not a characteristic root, then there is a
particular solution of the form
an (p) =(pt nt+ pt-1nt-1 +…+ p1n+p0) sn
(2) If s is a characteristic root with multiplicity m, then
there is a particular solution of the form
an (p) =nm (pt nt+ pt-1nt-1 +…+ p1n+p0) sn
•
Example7: what is the solution of the linear
nonhomogeneous relation an=6an-1-9an-2 +F(n)
(1) F(n)=n2 2n
(2) F(n)=3n (3) F(n)=n3
(1) Solution:
• let an (p) =(p2 n2 +p1 n+ p0) 2n .Then
(p2 n2 +p1 n+ p0) 2n= 6(p2 (n-1)2 +p1 (n-1)+ p0) 2n-19(p2 (n-2)2 +p1 (n-2)+ p0) 2n-2 + n2 2n
we have that p0= 192 p1=48 p2=4 .
• The characteristic root is r=3. hence
an=(b1+b2n)3n is a solution of an=6an-1-9an-2 .
Solving Recurrence Relations-2
• Definition1: The generating
function for the sequence a0,
a1, …, ak, … of real numbers
is the infinite series
G(x)= a0 + a1 x+ …+ak xk+…
• Example1: the generating function for the
sequences {ak} with ak=3, ak=2(k+1) and ak=2k
k
k
k
3
x
,
2(
k
1)
x
,
(2
x
)
are k 0
k 0
k 0
• Example2: what is the generating function for the
sequence 1,1,1,1,1?
• Solution: G(x)= 1+ x+ x2+x3 +x4
Useful Facts About Power Series
• Example3: the function
f(x)=1/(1-x)=1+ x+ x2+x3 +x4+ x5+…
is the generating functions of the sequence 1,1,…
the function
f(x)=1/(1-ax)=1+ ax+ a2 x2+… is the generating
functions of the sequence 1,a, a2,…
the function
f(x)=1/(1-x)2 =1+ 2x+ 3x2+4x3 +5x4+ 6x5+…
is the generating functions of the sequence
1,2,3, …, k+1, …
• Definition2: Let u be a real number and k a
nonnegative integer. Then the extended binomial
coefficient C(u,k) is defined by
u (u 1) (u k 1) / k ! if k 0
C (u, k )=
1
if k 0
• Exmaple4: C(-2,3)=-4 C(1/2,3)=1/16
• Exmaple5: when n<0 is an integer, then
n ( n)( n 1) ( n r 1)
r
r!
( 1) r n( n 1) ( n r 1)
r!
( 1) r ( n r 1)!
r n r 1
( 1)
r !( n 1)!
r
•
Threorem2: THE EXTENDED BINOMIAL THREOREM
Let x be a real number with -1<x<1 and u be a
real number . Then
u k
u
(1 x) x
k 0 k
•
Example6:
n
k
n
k n k 1 k
(1 x) x (1)
x
k
k 0 k
k 0
(1 x)
n
n k 1 k
x
k
k 0
Counting Problems and Generating
Functions
• Example7: Find the number of solutions of
e1+e2 +e3 =17, where e1, e2 and e3 are nonnegative
integers with 2e1 5, 3e2 6 and 4e1 7.
• Solution: the number of solutions with the
indicated constraints is the coefficient of x17 in the
expansions of:
(x2 + x3 + x4 + x5) (x3 + x4 + x5 +x6) (x4 + x5 + x6 + x7 )
This follows that the coefficient of x17 is 3.
• Example8: In how many different ways can eight
identical cookies be distributed among three
distinct children if each child receives at least two
cookies and no more than four cookies.
• Solution: the coefficient of x8 in the product
(x2 + x3 + x4)3 is 7.
• Example9: use generating functions to determine
the number of ways to insert tokens worth $1,
$2,and $5 into a vending machine to pay for an
item that costs r dollars in both the cases when the
order in which the tokens are inserted does not
matter and when the order does matter.
• Solution: case1: no order is considered
the answer is the coefficient of xr in the generating
function (1+x+x2 + …)(1 +x2 +x4+ …)(1+x5 +x10 + …)
• case2: when the order does matter, then the
number of ways to insert exactly n tokens to
produce a total of r dollars is the coefficient of
xr in the generating function (x+x2 + x5)n , since
each of the r tokens may be a $1 token, a $2
token, or a $5 token. Since any number tokens
may be inserted, the number of ways to
produce r dollars is the coefficient of xr in
1+ (x+x2 + x5)+ (x+x2 + x5)2 +…=1/1- (x+x2 + x5)
• Example10: use generating function to find the
number of k-combinations of a set with n elements.
Assume that the Binomial Theorem has been
established.
• Solution: each of the n elements in the set
contributes the term (1+x) to the generating function
f(x)=(1+x)n , by the binomial theorem , we have
n k
f ( x) k 0 x
k
n!
n
C (n, k )
k k !(n k )!
n
hence
• Example11: use generating function to find the
number of r-combinations from a set with n
elements when repetition of elements is allowed.
• Solution: Let G(x)=(1+x+x2 +…)n, then the
coefficient of xr is the answer. Hence
G(x)=(1+x+x2 +…)n=(1+x)-n=C(n+r-1,r)xr
Using Generating Functions TO
Solve Recurrence Relations
• Example12: solve the recurrence relation
an=6an-1-9an-2 with a0=1 and a1=6.
• Solution: let G(x)= an x n , Then
n 0
G ( x) n 2 an x 1 6 x n 2 (6an 1 9an 2 ) x n
n
6 x n 0 an x 9 x
n
2
(6 x 9 x 2 )G ( x) 1
n 0
an x 1
n
Using the recurrence relation, we have
1
G ( x)
2
1 6x 9x
2
1
n n
n 0 ( )(3) x
2
n
(1 3x)
n0 (n 1)3 x
n
n
• Example13: Solve the recurrence relation
an=8an-1+10n-1 with a1=9.
• Solution: Let G ( x) ak x k
k 0
then G ( x) 1 (8ak 10k 1 ) x k
k 1
8 x ak x x 10
k
k 0
k 1
x
8 xG ( x)
1 10 x
k 1
x
k 1
Hence we have
1 9x
G ( x)
(1 8 x)(1 10 x)
1
1
1
(
)
2 1 8 x 1 10 x
1
n
n
n
k 0 (8 +10 ) x
2
Inclusion-Exclusion
• The Principle of Inclusion-Exclusion
• Theorem1: Let A1, A2 , … , An be finite sets.
Then A
A
A
1
2
1i n
Ai
1i j k n
( 1)
n
n 1
1i j n
Ai
Aj
A1
A2
Ai
Aj
Ak
An
1 An Alternative Form of InclusionExclusion
• Let Ai be the subset containing the elements that
property Pi . The number of elements with all
the properties Pi1, Pi2 , … , Pik will be denoted
by N(Pi1Pi2 … Pik ). Writing these quantities in
terms of sets, we have
Ai1 Ai2
Aik N ( Pi1 Pi2 Pik )
If the number of elements with none of the
properties P1,P2 ,…, Pn , is denoted by
N ( PP
Pn ) and the number of elements
1 2
in the set is denoted by N.
From the Principle of Inclusion-Exclusion, we
see that
N ( PP
1 2
Pn ) N A1 A2
N N ( Pi )
1i n
1i j n
(1) N ( PP
1 2
n
N ( PP
i j)
Pn )
An
1i j k n
N ( PP
i j Pk )
• Example1: how many solutions does
x1+x2+x3=11 have, where x1 , x2 and x3 are
nonnegative integers with x1 , x2 and
x3
• Solution: let P1 denote the property of element
of the set that x1,and P2 : x2 , P3: x3.
Then
N ( PP
1 2 P3 ) N N ( P1 ) N ( P2 ) N ( P3 )
N ( PP
1 2 ) N ( PP
1 3 ) N ( P2 P3 ) N ( PP
1 2 P3 )
•
•
•
•
•
•
•
•
N=C(3+11-1,11)=78
N(P1)=C(3+7-1,7)=36
N(P2)=C(3+6-1,6)=28
N(P3)=C(3+4-1,4)=15
N(P1P2)=C(3+2-1,2)=6
N(P1P3)=C(3+0-1,0)=1
N(P2P3)=0
N(P1P2 P3)=0
• N ( PP
1 2 P3 ) =6
THE SIEVE OF ERATOSTHENES
• To find the number of primes not to exceeding a
specified positive integer.
• For instance, to find the number of primes not
to exceeding 100.
• Note that a composite integer not to exceeding
100 must have a prime factor not to exceeding
10.
• The primes not to exceeding 100 are divisible by
none of 2,3,5 and 7.
• Let P1, P2, P3, P4 denote an integer is divisible
by 2,3 5,7 respectively.
• Then the number of primes not to exceeding 100
is 4 N ( PP
1 2 P3 P4 )
N ( PP
1 2 P3 P4 ) 99 N ( P1 ) N ( P2 ) N ( P3 ) N ( P4 )
N ( PP
1 2 ) N ( PP
1 3 ) N ( PP
1 4 ) N ( P2 P3 ) N ( P2 P4 )
N ( P3 P4 ) N ( PP
1 2 P3 ) N ( PP
1 2 P4 ) N ( P2 P3 P4 )
N ( PP
1 2 P3 P4 )
99 50 33 20 14 16 10 7 6 4 2
3 2 1 0 0 21
The Number of Onto Functions
• Example2: how many onto functions are there from
a set with six elements to a set with three elements?
• Solution: assume that the elements in the codomain
are b1, b2, b3. let P1,P2,P3 be the properties that b1, b2
and b3 are not in the range of the function,
respectively. note that a function is onto if and only
if it has none of the properties P1,P2 and P3. hence
N ( P1P2P3) N N ( P1 ) N ( P2 ) N ( P3 )
N ( P1P2 ) N ( P1P3 ) N ( P2 P3 ) N ( P1P2 P3 )
36 C (3,1)26 C (3, 2)16 540
• Theorem1: let m and n be positive integers
with mn. Then , there are
n C (n,1)(n 1) C (n, 2)(n 2)
m
m
n1
m
(1) C (n, n 1)1
m
Onto functions from a set with m elements to a
set with n elements.
Derangements
• Example3: The Hatcheck Problem
A new employee checks the hats of n people at a
restaurant, forgetting to put claim check
numbers on the hats. When customers return for
their hats, the checker gives them back hats at
random from the remaining hats. What is the
probability that no one receives the correct hat?
• Remark: the answer is the number of ways the
hats can be arranged so that there is no hat in its
original position divided by n!.
• Definition: a derangement is a permutation of
objects that no object in its original position.
• For example: 21453 is a derangement of 12345.
• Let Dn denote the number of derangement of n
objects.
• Theorem2: the number of derangements of a
set with n elements is
1 1 1
Dn n!(1
1! 2! 3!
1
(1) )
n!
n
• Proof: let a permutation have property Pi if it
fixes element i. The number of derangements
is the number of permutations having none of
the properties Pi for i=1,2,…, n. This means
that
Dn N ( P1P2
Pn )
• Using the principle of inclusion-exclusion, it
follows that
N ( PP
1 2
Pn ) N A1
n! N ( Pi )
1i n
1i j n
(1) n N ( PP
1 2
A2
N ( PP
i j)
Pn )
An
1i j k n
N ( PP
i j Pk )
• We can see that
• N(Pi)=(n-1)!
• N(Pi Pj)=(n-2)!
• ……
• N(Pi1 Pi2 … Pim )=(n-m)!
• And
N ( Pi ) C ( n,1)( n 1)!
1 i n
1 i j n
N ( Pi Pj ) C ( n, 2)( n 2)!
• And in general,
1 i1 i2
im n
N ( Pi1 Pi 2
Pim ) C (n, m)(n m)!
• Hence we have
Dn n ! C (n,1)(n 1)! C (n, 2)(n 2)!
(1) n (n n)!
n!
n!
n !
(n 1)!
(n 2)!
1!(n 1)!
2!(n 2)!
1 1
n 1
n ![1 (1) ]
1! 2!
n!
n!
(1)
(n n)!
0! n!
n
Table1 the probability of a derangement
n
2
3
4
5
6
7
0.375
0.367
Dn /n! 0.5000 0.3333
0.3667 0.3681
0
8