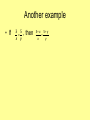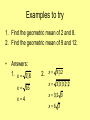Download Ratio and Proportion

Ratio and Proportion
Unit 6
Ratio of a to b
• If a and b are two quantities that are
measured in the same units, then the ratio of
a
a to b is
.
b
• The ratio of a to b can also be written as a:b
• Ratios should be written in their simplified
form with a and b as integers.
Some examples
5 ft 5

2yd 6
because there are 3 feet in 1 yard
3oz 3oz
3


4lb 64oz 64 because there are 16 ounces in a pound
Proportion Word Problems
• The perimeter of the isosceles triangle
shown is 56 in. The ratio of LM:MN is 5:4.
Find the lengths of the sides and the base
L
of the triangle.
N  M
The perimeter = LM + MN + LN so 56 = LM + MN + LN
The ratio of LM:MN is 5:4 so let LM = 5x and MN = 4x
56 = LM + MN + LN
56 = 5x + 4x + 5x
56 = 14x
4=x
so LM = 20, MN = 16, LN = 20
N
M
Here is one for you to try:
• The perimeter of a rectangle is 40 in. The
ratio of the length to the width is 3:2. Find
the length of BC and CD.
The perimeter = 2(length) + 2(width). The
perimeter is 40 in.
2CD + 2BC = 40
Let length = 3x and width = 2x
2(3x) + 2(2x) = 40
6x + 4x = 40
10x = 40
X=4
Length CD = 12 and width BC = 8
A
B
D
C
Here is another example:
• The measures of the angles in a triangle
are in the extended ratio 3:4:8. Find the
measures of the angles.
Let the angle measures be represented by 3x, 4x, and 8x.
The sum of the measures of a triangle is 1800 , so
3x + 4x + 8x = 180
Proportions
• A proportion is an equation that sets two
ratios equal to each other.
a c

b d
The numbers a and d are the extremes.
The numbers c and d are the means.
Solving a Proportion
• Cross Multiply to solve a proportion.
If
a c

b d
, then ad = bc
This is sometimes referred to as
The product of the extremes = the product of
the means.
Let’s see some examples
• Solve the proportions
x 14

6 9
4 7

x 5
ans:
9 x  84
84
x
9
28
x
3
ans:
20  7 x
20
x
7
20
x
7
Here is one a bit more complicated
x 5 x

4
10
10( x  5)  4 x
10 x  50  4 x
50  6 x
50
x
6
50
x
6
25
x
3
Be careful, the numerator is an
algebraic expression.
Make sure to put it into parentheses
when cross multiplying.
Here is one for you to try:
3 x x

6
2
2(3  x )  6 x
6  2x  6 x
6  8x
6
x
8
6
x
8
3
x
4
Additional Properties of Proportions
• If
a c , then

b d
• If
a c , then a  b c  d


b
d
b d
a b

c d
Okay, so what do we do with those
properties?
• Is the statement true or false?
• If
x 15

10 y
, then
x 3

y 2
• Check by cross multiplying both and see if
they are the same.
• xy  15
2x=3y
• Not the same so this is a false statement
Another example
• If
3 5

x y
, then
3 x 5 y

x
y
Geometric Mean
• The geometric mean of two positive
numbers a and b is the positive number x
a
x
such that 
x
x = ab
b
Examples
• Find the geometric mean between
16 and 4.
Solution:
16 x

x 4
x 2  64
x 8
Examples to try
1. Find the geometric mean of 2 and 8.
2. Find the geometric mean of 9 and 12.
•
Answers:
1. x  2 8
x  16
x4
2. x  9 12
x 33322
x 3 2 3
x 6 3