Download ITrig 2.4 - Souderton Math

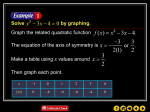
A Library of Parent Functions
Objective: To identify the graphs
of several parent functions.
Example 1
• Write the linear function f for which f(1) = 3 and
f(4) = 0.
Writing a Linear Function
• Write the linear function f for which f(1) = 3 and
f(4) = 0.
• Remember, f(1) = 3 means when x = 1, y = 3
and f(4) = 0 means when x = 4, y = 0. We have
two points. We will treat this like a line and find
its equation.
Example 1
• Write the linear function f for which f(1) = 3 and
f(4) = 0.
• Remember, f(1) = 3 means when x = 1, y = 3
and f(4) = 0 means when x = 4, y = 0. We have
two points. We will treat this like a line and find
its equation.
m
03
 1
4 1
y  3  1( x  1)
or
f ( x)   x  4
You Try
• Write the linear function f for which f(2) = 5 and
f(1) = 2.
You Try
• Write the linear function f for which f(2) = 5 and
f(1) = 2.
52
m
3
2 1
y  5  3( x  2)
or
f ( x)  3x  1
Squaring Function
•
We have talked about the look of a 2nd degree
equation and we have called it a parabola.
Here are some characteristics.
1. The domain is all real numbers, and the range
is either (, max) or (min, ) .
Squaring Function
•
We have talked about the look of a 2nd degree
equation and we have called it a parabola.
Here are some characteristics.
1. The domain is all real numbers, and the range
is either (, max) or (min, ) .
2. If the coefficient of x 2 is positive, it opens up
and if the coefficient is negative, it opens
down.
Squaring Function
•
We have talked about the look of a 2nd degree
equation and we have called it a parabola.
Here are some characteristics.
1. The domain is all real numbers, and the range
is either (, max) or (min, ) .
2. If the coefficient of x 2 is positive, it opens up
and if the coefficient is negative, it opens
down.
3. It can have zero, one, or two x-intercepts.
Squaring Function
No real roots
(2 imaginary)
Two real roots
One real root
(double root)
The Cubic Function
•
We have also talked about a third degree
equation and what it looks like. Here are some
of its characteristics.
1. The domain and range are all real numbers.
The Cubic Function
•
We have also talked about a third degree
equation and what it looks like. Here are some
of its characteristics.
1. The domain and range are all real numbers.
3
2. If the coefficient of x is positive, it ends up
and to the right and if it is negative, it ends
down and to the right.
The Cubic Function
•
We have also talked about a third degree
equation and what it looks like. Here are some
of its characteristics.
1. The domain and range are all real numbers.
3
2. If the coefficient of x is positive, it ends up
and to the right and if it is negative, it ends
down and to the right.
3. It can have one, two, or three x-intercepts.
The Cubic Function
One real root
(2 imaginary)
Three real roots
Two real roots
(1 double root)
The Square Root Function
• We will take a look at the square root function.
This is something that you should recognize and
we will talk about it in more depth later.
The Absolute Value Function
• This is another function that you should
recognize. We will do more with it later.
Graphing a Piecewise-Defined
Function
• Sketch the graph of
2x  3 x  1
f ( x) 
 x  4 x 1
Graphing a Piecewise-Defined
Function
• Sketch the graph of
2x  3 x  1
f ( x) 
 x  4 x 1
x y
-1 1
0 3
1 5
Graphing a Piecewise-Defined
Function
• Sketch the graph of
2x  3 x  1
f ( x) 
 x  4 x 1
x y
-1 1
0 3
1 5
x
1
2
3
y
3
2
1


Graphing a Piecewise-Defined
Function
• You try:
• Sketch the graph of
 x2
f ( x) 
2x 1
x  1
x  1
Graphing a Piecewise-Defined
Function
• You try:
• Sketch the graph of
 x2
f ( x) 
2x 1
x y
-3 1
-2 0
-1
-1
x  1
x  1
x y
-1 -1
0
1
1
3
Homework
• Page 220
• 1-5, 43, 53-59 odd