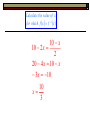Download Solving Quadratics

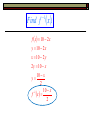
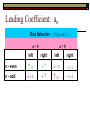
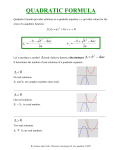
Solving Quadratics
Quadratic Formula
Discriminant – Nature of the Roots
Warm Up – Question 1

Given
f : x  x  4 x, x  
2

and
1
g:x
x3

find an expression for the composite function
g  f xand
 state its domain restrictions.
Warm Up Answer
1
g  f x   2
x  4x  3
1

,
x  1x  3
x  1 x  3
Warm Up – Question 2

Given
f ( x )  10  2 x , x   , x  0
1
x.
a)
Find f
b)
Calculate the value of x
for which f x   f
1
x .
Find f
1
 x .
f  x   10  2 x
y  10  2 x
x  10  2 y
2 y  10  x
10  x
y
2
10  x
1
f x  
2
Calculate the value of x
for which f  x   f 1  x .
10  x
10  2 x 
2
20  4 x  10  x
 3 x  10
10
x
3
Solve by Quadratic
Formula
 b  b  4ac
x
2a
2
Derive the Quadratic Formula
by Completing the Square
ax 2  bx  c  0
ax 2  bx  c
 2 b 
a  x  x   c
a 

2
2
 2 b

b
b


a x  x      c 

a
4a
 2a  

b 
 4ac  b 2

a x   
2a 
4a

2
b 
b  4ac

x




2
a
4a 2


2
2
b 
b 2  4ac

x  
2
2a 
4a

2
b
b 2  4ac
x

2a
4a 2
b
b 2  4ac
x 
2a
2a
 b  b 2  4ac
x
2a
Solve using the Quadratic Formula
x  5 x  14  0
2
 b  b 2  4ac
x
2a
 5  25  41 14 
x
21
 5  25  56
x
2
 5  81
x
2
a 1
b5
c  14
59 4
x
 2
2
2
 5  9  14
x

 7
2
2
Solve using the Quadratic Formula
4 x  8  3x
4 x  3x  8  0
2
2
 b  b 2  4ac
x
2a
 3  9  44  8
x
24 
 3  9  128
x
8
 3  137
x
8
a4
b3
c  8
Solve using the Quadratic Formula
2
a3
9  3x  0
3x  9  0
2
 b  b 2  4ac
x
2a
0  0  43 9
x
23
0  0  108
6
 108
x
6
x
b0
c  9
6 3
x
 3
6
6 3
x
 3
6
Solve using the Quadratic Formula
10  5 x  15 x  0
2
a  1, b  3, c   2


5 x 2  15 x  10  0  5 x 2  3 x  2  0
 b  b 2  4ac
x
2a
 3  9  41 2
x
21
3 98
2
 3  17
x
2
x
Solve using the Quadratic Formula
2 x  3x  1  2 x  3x  1  0
2
2
a2
 b  b  4ac
x
2a
3  9  421
x
22
b  3
c 1
2
3  1 3 1
x

4
4
3 1 4
x
 1
4
4
3 1 2 1
x
 
4
4 2
Solve using the Quadratic Formula
 2 x  3 x  1  0  Same as previous but signs change
2
a  2
b3
c  1
 b  b 2  4ac
x
2a
 3  9  4 2 1
x
2 2
 3  1  3 1
x

4
4
 3 1  2 1
x


4
4 2
 3 1  4
x

1
4
4
Solve using the Quadratic Formula
 x  6 x  2  f x    x  6 x  2  0
2
a  1
b6
c2
2
 b  b 2  4ac
x
2a
 6  36  4 12
x
2 1
 6  44  6  2 11

2
2
2  3  11
x
 1  3  11
2
x  3  11
x




Solve using the Quadratic Formula
2x  x  2  x  2x  2  0
2
a 1
b2
c  2
2
 b  b 2  4ac
x
2a
 2  4  4 1 2 
x
21
 2  12  2  2 3
x

2
2
2 1 3
x
 1  3
2


The Discriminant  
The nature of the roots
The Discriminant

It comes from the quadratic formula.
 b  b  4ac
x
2a
2

  =

b  4 ac
2

When you apply the quadratic formula to any
quadratic equation, you will find that the
value of b²-4ac is either positive, negative, or
0.

The value of the discriminant is what tells us
the nature of the roots (solutions) to the
quadratic.
Solutions of a Quadratic Equation
If

b  4 ac  0 
2
2 real solutions
( Rational or Irrational )
b  4 ac  0 
2
b  4 ac  0 
2
1 real solution
( Rational )
0 real solutions
Has imaginary roots
Real Numbers (ℝ)
Rational Numbers (ℚ)
Integers (ℤ)
Whole Numbers
Natural Numbers (ℕ)
1, 2, 3, …
0, 1, 2, 3, …
…-3, -2, -1, 0, 1, 2, 3,
…
Decimal form either
terminates or repeats
All rational and irrational numbers
Irrational Numbers
Decimal form is
non-terminating
and non-repeating
Find the Discriminant and Describe its
Roots. 2 x 2  4 x  2  0
 
b  4ac
2
4  422
2
16  16
0

Nature of the Roots
1 real solution
Rational
Find the Discriminant and Describe its
Roots. 2 x 2  4 x  1  0
 
b  4ac
2
4  42 1
2
16  8
8

Nature of the Roots
2 real solutions
Rational
Find the Discriminant and Describe its
2
Roots 2 x  4 x  3  0
 
2
b  4ac
4  423
2
16  24
8

Nature of the Roots
No real solutions
(imaginary )
Graphs of Polynomial
Functions
Explore – Look at the relationship between the degree & sign of the
leading coefficient and the right- and left-hand behavior of the graph of
the function.
y  x3  2 x 2  x  1
y  2 x  3x  4
y  2 x5  2 x 2  5 x  1
y  x 4  3x 2  2 x  1
y  2 x  x  5 x  3
y   x 2  3x  2
y   x3  5 x  2
y   x  x  5x  4
5
2
2
6
2
Explore – Look at the relationship between the degree & sign of the leading
coefficient and the right- and left-hand behavior of the graph of the function.
y  x3  2 x 2  x  1
y  2 x  3x  4
y  2 x5  2 x 2  5 x  1
y  x 4  3x 2  2 x  1
y  2 x  x  5 x  3
y   x 2  3x  2
y   x3  5 x  2
y   x  x  5x  4
5
2
2
6
2
Explore – Look at the relationship between the degree & sign of the leading
coefficient and the right- and left-hand behavior of the graph of the function.
y  x  2x  x  1
y  2 x  3x  4
y  2 x  2 x  5x  1
y  x 4  3x 2  2 x  1
y  2 x  x  5 x  3
y   x 2  3x  2
y   x3  5 x  2
y   x  x  5x  4
3
2
5
2
5
2
2
6
2
Continuous Function

A function is continuous if its graph can be
drawn with a pencil without lifting the pencil
from the paper.
Continuous
Not Continuous
Polynomial Function

Polynomial Functions have continuous graphs
with smooth rounded turns.

Written:
f ( x)  an x n  ax 1 x n 1 

Example:
5
4
3
2
f ( x)  4 x  8 x  2 x  7 x  8 x  2
 a2 x 2  a1 x  a0
Explore using graphing Calculator
Describe graph as S or W shaped.
Function
Degree
# of U turns
y  x2  x  2
2
1W
y  3x3  12 x  4
3
2S
3
2S
4
3 W
4
3 W
3
2S
y  x3  3x 2  3x  1
3
2S
y  x 4  2x 3  x 2  x  1
4
3 W
y  2 x3  4 x 2  x  2
y  x 4  5 x3  5 x 2  x  6
y  x 4  2 x3  5 x 2  6 x
y  x3
Generalizations?

The number of turns is one less than the
degree.

Even degree → “W” Shape

Odd degree → “S” Shape
Describe the Shape and Number of
Turns.
b x   x 3  4 x 2  2 x  8
S, 2
m x   x 4  4 x 2  2 x  8
W, 3
s x   2 x 3  x 2  10 x  5
S, 2
k x    x 4  2 x 3  13 x 2  14 x  24
W, 3
Let’s explore some more….we might
need to revise our generalization.

Take a look at the following graph and tell me
if your conjecture is correct.
yx
4
Let ' s revise our conjecture :
The number of U turns is
less than or equal to one
less than the Degree.
There is only a turn
when the function changes
from inc to dec or dec to inc
and indicates a max or a min .
Lead Coefficient Test
When n is odd
Lead Coefficient is Positive: (an
>0), the graph falls to the left and
rises to the right
as x  , f ( x)  
as x  , f ( x)  
Lead Coefficient is Negative: (an
<0), the graph rises to the left and
falls to the right
as x  , f ( x)  
as x  , f ( x)  
Lead Coefficient Test
When n is even
Lead Coefficient is Positive: (an
>0), the graph rises to the left and
rises to the right
as x  , f ( x)  
as x  , f ( x)  
Lead Coefficient is Negative: (an
<0), the graph falls to the left and
falls to the right
as x  , f ( x)  
as x  , f ( x)  
Leading Coefficient: an
End Behavior - f ( x)  ax n  ...
a>0
a<0
left
right
left
right
n - even


 

n - odd
 



Use the Leading Coeffiicent Test to describe the right-hand and
left-hand behavior of the graph of each polynomial function:
f ( x)   x  2 x  5
3
As x  , f x    
As x  , f x   
Use the Leading Coeffiicent Test to describe the right-hand and
left-hand behavior of the graph of each polynomial function:
f ( x)  x  9 x  5 x  2 x  3 x  1
6
5
4
As x  , f x   
As x  , f x   
2
Use the Leading Coeffiicent Test to describe the right-hand and
left-hand behavior of the graph of each polynomial function:
f ( x)  x  2 x  3 x  2 x  4
5
4
3
As x  , f x   
As x  , f x    
Use the Leading Coeffiicent Test to describe the right-hand and
left-hand behavior of the graph of each polynomial function:
f ( x)   x  2 x  5 x  2
4
3
As x  , f x    
As x  , f x    
A polynomial function (f) of degree n , the
following are true

The function has at most n real zeros

The graph has at most (n-1) relative extrema
(relative max/min)
Local Max / Min (in terms of y)
Increasing / Decreasing (in terms of x)
f ( x)  x  2 x  3 x  6 x  2
4
3
2
Local Max / Min (in terms of y)
Increasing / Decreasing (in terms of x)
.73, .29
1.9,  2.1

 1.1,  8.1

Min  8.1,  2.1
y

Max  0.29


f ( x)  x 4  2 x 3  3 x 2  6 x  2
NOTE :  means ' or '
 Inc :  1.1,0.73  1.9,   
x

 Dec :  ,1.1  0.73,1.9 
Approximate any local maxima or minima to the nearest tenth.
Find the intervals over which the function is increasing and
decreasing.
 2.5, 3.1

1.45,1.4


 0.23,  0.06 

f x   0.15x 4  0.25x 3  x 2  0.5x
Max  3.1,1.4 x   Inc :  ,2.5   0.23,1.45


y

Dec :  2.5,  0.23  1.45,   

Min


0
.
06


Find the Zeros of the polynomial function below and
sketch on the graph:
f ( x)  x  x  12 x
3
0  x3  x 2  12 x


0  x x  x  12
0  xx  4x  3
2
x  0 x  4
x3
2
Find the Zeros of the polynomial function below and
sketch on the graph:
f ( x)  x  4 x  4
2
0  x  4x  4
2
0  x  2x  2
x  2
Multiplicity of 2 – EVEN - Touches
Find the Zeros of the polynomial function below and
sketch on the graph:
f ( x)  x  2 x  16 x  32
3
0  x 3  2 x 2  16 x  32
0  x 2  x  2   16 x  2 


0  x 2  16  x  2 
0   x  4  x  4  x  2 
x  4
x4
x  2
2
Find the Zeros of the polynomial function below and
sketch on the graph:
f ( x)  3 x  2 x  5
2
x
x
x
x
 b  b 2  4ac
2a
2  4  435
6
2  4  60
6
2   56
6
NO X-INTERCEPTS!
Find the Zeros of the polynomial function below and
sketch on the graph:
5 2 8
4
f ( x)  x  x 
3
3
3
5 2 8
4
0 x  x
3
3
3
Multiply Both Sides by 3.
0  5x2  8x  4
0  x  25 x  2
x  2
2
x  or 0.4
5