* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Absolute Value Inequalities
Survey
Document related concepts
Transcript
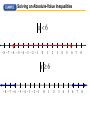
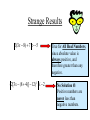
Absolute Value Inequalities Algebra Solving an Absolute-Value Inequalities x 6 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 x 6 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 Graphing Absolute Value • When an absolute value is greater than the variable you have a disjunction to graph. x 4 • When an absolute value is less than the variable you have a conjunction to graph. x 4 Solving an Absolute-Value Inequality Solve | x 4 | < 3 x 4 IS POSITIVE |x4|3 x 4 3 x7 x 4 IS NEGATIVE |x4|3 x 4 3 x1 Reverse inequality symbol. The solution is all real numbers greater than 1 and less than 7. This can be written as 1 x 7. Solving an Absolute-Value Inequality Solve 1POSITIVE | 3 6 and graph 2x +| 2x 1 IS 2x +the1solution. IS NEGATIVE | 2x 1 | 3 6 2x + 1 IS POSITIVE | 2x|2x 1| 31 |6 9 2x 1 |1 | 2x 9 +9 | 2x 1 | 3 6 2x + 1 IS NEGATIVE | 2x|2x 1| 31 |6 9 2x 1 9 | 2x 1 | 9 2x 10 2x 1 9 x 5 2x 8 x4 2x 1 +9 2x 10 2x 8 The solution is all real numbers greater than or equal x4 x 5 to 4 or less than or equal Reverse to 5. This can be written as the compound inequality inequality x 5 or x 4. symbol. 6 5 4 3 2 1 0 1 2 3 4 5 6 Strange Results 2(3x 8) 7 5 (2[3x (8 4)] 12)3 2 True for All Real Numbers, since absolute value is always positive, and therefore greater than any negative. No Solution Ø. Positive numbers are never less than negative numbers. Absolute Value Inequalities Algebra