Download Verdana 30 pt

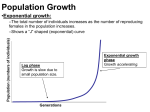
Liceo Scientifico “Isaac Newton”
Roma
Y
School Year 2011-2012
Maths course
(0,1)
Exponential function
O
X
Compound interest
M1= C + C i = C ( 1 + i )
M2 = M 1 + M1 i = M 1 ( 1 + i ) = C ( 1 + i )²
Sum of money
M=C(1+i)
x
where the variable x can indicate also fractional values of time.
(1+i)>1
It’s great!
General exponential function
y=a
x
a>0
xєR
Its domain is the set of real numbers R, while its codomain is the
set of real positive numbers R +
a>1
0<a<1
a=1
First condition
If
x
-3
-2
a>1
x
y=2
Y
y
1
8
1
4
-1
1
2
0
1
1
2
(0,1)
2
4
3
8
O
1
X
Y
Key:
y=2
y=3
x
x
(0,1)
O
1
X
Second condition
if 0 < a < 1
Y
x
y
-3
8
-2
4
-1
2
0
1
1
1
2
2
1
4
3
1
8
-x
y=2
(0,1)
O
1
X
Y
Key:
y=2
y=3
-x
-x
(0,1)
O
1
X
Third condition
If a = 1
Y
(0,1)
O
y=1
1
X
The symmetry about the y axis
Y
Key:
y=2
y=2
x
-x
(0,1)
O
1
X
This property is true for every pair of exponential functions of this
type:
y=a
x
y=a
-x
In fact if we apply the equations of symmetry about the y axis to
x
the function y = a we obtain the following curve:
y=a
x
X=-x
Y= y
-x
Y=a
Properties of the exponential function
the injectivity
the surjectivity
the exponential function is bijective
so it’s invertible
Logarithmic function
y=a
Y
x
y=x
If a > 1
y = log x
a
(0,1)
O
(1,0)
X
Logarithmic function
Y
y=a
x
y=x
If 0 < a < 1
(0,1)
O
(1,0)
X
y = log x
a
a>1
the exponential function grows
faster than any polynomial function
DEFINITION
Let C and C’ be two curves both passing through a
point P; we say that C is steeper than C’ in P if the
slope of the tangent in P to C is greater than the
one of the tangent in P to C’.
Key:
2
y=x+2x+1
y = ln2 ∙ x + 1
Y
y=2x+1
y=2
x
(0,1)
O
P
1
X
Euler‘s number e
Values of a
Exponential
function
x
a=2
y=2
a = 2.5
y = 2.5
a = 2.7
y = 2.7
a = 2.71
y = 2.71
Slope m
m = 0.6931
x
m = 0.9933
x
y = 2.718
a = 2.719
y = 2.719
a ≤ 2.718 then m < 1,
m = 0.9163
x
a = 2.718
If a grows, m also grows
m = 0.9969
x
x
m = 0.9999
m = 1.0003
a ≥ 2.719 then m > 1;
this means that there’s a value
of a between these two values
for which the slope of the
tangent in P is equal to 1.
This number is called Euler’s number e in honour of the
mathematician who discovered it.
It is an irrational number and a transcendental number because
it isn’t the solution of any polynomial equation with rational
coefficients.
e = 2.7
The exponential function having base equals e is called a natural
exponential function and its equation is:
y=e
x
Y
y=e
x
Key:
y=e
x
y=x+1
y=x+1
(0,1)
45 °
O
1
X
Graphs of non-elementary exponential functions:
1) symmetries, 2) translations, 3) dilations or compressions.
1) if we apply the equations of the symmetry about the x axis to
the function y = a x we obtain the following curve:
y=a
x
X=
x
Y=-y
Y=-a
x
2) if we apply the equations of a translation by a vector v having
x
components (h,k) to the function y = a we obtain the following
curve:
y=a
X=x+h
x
Y=y+k
Y–k=a
X-h
X-h
Y=a
+ k
3) if we apply the equations of a dilation to the function y = a
obtain the following curve:
x
X
y=a
x
X=hx
Y
Y=ky
k
= ah
we
Examples of graphs:
x
y=2 +1
x
1) the equation y = 2 + 1
x
represents the curve y = 2
shifted up by one:
Y
x
y=2
Key:
y=2
y=2
x
x
+1
(0,1)
O
y=1
1
X
x+1
2) the equation y = 2
x
represents the curve y = 2
shifted one point to the left:
x+1
y=2
Y
x
y=2
Key:
y=2
y=2
x
x+1
(0,1)
O
1
X
x-3
3) the equation y = 2 - 2 x
represents the curve y = 2
shifted three points to the
right and shifted down by
two:
Y
Key:
y=2
y=2
x
x-3
- 2
x
y=2
(0,1)
x-3
y=2
O
1
- 2
X
y = -2
x
4) the equation y = 3 ∙ 2
x
represents the curve y = 2
in which the abscissas don’t
change while the ordinates
are tripled:
Y
y=3∙2
x
x
y=2
Key:
y=2
x
y=3∙2
x
(0,1)
O
1
X
x
5) the equation y = 2 3
x
represents the curve y = 2
in which the ordinates don’t
change while the abscissas
are tripled:
Y
x
y=2
Key:
y=2
x
x
y=2
y=2
3
(0,1)
O
1
X
x
3
x
6) the equation y = 2
represents two curves:
y=2
x
Y
if x ≥ 0
-x
y=2
-x
x
y=2
y=2
if x < 0
Key:
y=2
y=2
x
-x
(0,1)
O
1
X
x+1
7) the equation y = 2
represents two curves:
Y
y=2
x+1
-x-1
y=2
if x ≥ -1
if x < -1
Key:
y=2
x +1
- x -1
y=2
(0,1)
-1
O
1
X
x+1
8) the equation y = 2
-1
represents the graph of the
previous curve number 7
shifted down by one:
Y
Key:
y=2
y=2
x +1
-1
- x -1
-1
(0,1)
-1
O
1
X
x+1
9) the equation y = - 2 + 1
can be rewritten as follows:
y=-(2
Y
x+1
-1)
this equation represents
the symmetrical curve of the
function y = 2 x + 1 - 1 about
the x axis
Key:
y=2
(0,1)
O
x +1
-1
x +1
y = - (2
-1)
(0,-1)
1
X
10) the equation
y=2
x+1
y=2
x+1
-2
-2
Y
the part of the negative ordinates is
substituted by its mirror image about
the x axis:
(0,1)
O
1
X
.
Copyright 2012 © eni S.p.A.