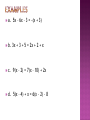Download Slide 1

Math 021

An equation is defined as two algebraic expressions
separated by an = sign.

The solution to an equation is a number that when
substituted into the equation makes it a true
statement.

For example, 8 is a solution to the equation x2 – 9x = -8 since
when x = 8 the equation becomes:
82 – 9(8) = -8
64 – 72 = -8
-8 = -8
which is a true statement
However, 2 is not a solution since:
22 – 9(2) = -8
4 – 18 = -8
-14 = -8
which is a false statement
A
linear equation in one
variable is any equation which
contains a single variable and
that variable is raised to the
first power.
The general form of a linear
equation in one variable is ax +
b = c where a, b, and c are real
numbers.


Let a, b, c be real numbers. If a = b, then a + c = b +
c. The addition property allows you to add or subtract
any term from both sides of an equation and the
equation will remain equal.
Examples – Solve the following using the addition
property:
a. x + 3 = 7 + 8
b. 5x = 16 + 4x
c. 7x - 5 = 8x + 10
d. 10x – 5x = 4x – 11
e. 2(x + 6) = x – 3
f. 3(4x – 11) = -11(3 – x)
 Let
a, b, c be real numbers, If a = b, then
a∙c = b∙c. The multiplication property allows
you to multiply or divide any non-zero
number to both sides of an equation and the
equation will remain equal.
 Examples – Solve the following using the
multiplication property:
a. 7x = 35
b. 5x + 6x = 39 + 5
c. -16(1-x) – 14x = –10
d. 5x – 4 = 26 + 2x
e. 8x – 5x + 3 = x – 7 + 10
f. -2(5x – 1) – x = -4(x – 3)
 Multiply
by a LCD to eliminate any fractions
or multiply by a power of 10 to eliminate
decimals
 Use the distributive property if necessary
 Combine like terms on the same side of the
equal sign
 Use the addition property to isolate the term
containing the variable on one side of the
equation and the real number to the other
 Solve for the variable by using the
multiplication property
 Examples
– Solve each of the following:
5
2
a.
b.
2
7 11
 x
x

4
7
5
30 15
c. 1 x  2  1 x  1
2
3
6
12
d.
5( x  1)
4
= 3( x  1)
2
 e.

0.5x – 0.3 = 1.1 + 0.3x
f. 0.15(4 – x) = 0.13(2 – x)
A
contradiction is a statement in
mathematics that when completely
simplified is false. A linear equation that
simplifies to a contradiction has no solution.
 An
identity is a statement in mathematics
that when completely simplified is always
true. A linear equation that simplifies to an
identity has an infinite number of solutions,
or all real numbers.
 a.
5x – 6x – 3 = -(x + 3)
 b.
3x + 3 + 5 = 2x + 2 + x
 c.
9(x – 2) = 7(x – 10) + 2x
 d.
5(x – 4) + x = 6(x – 2) – 8
An absolute value equation is any equation
that contains one or more absolute values.
 To eliminate absolute values, use the
definition that if |x| = c, then x = c or x = -c
 Examples – Solve each of the following:
 a. |x + 3| = 7
b. |x + 3| – 4 = 7

 c.
 e.
|2x – 5| + 1 = 6
|3x + 1| + 10 = 6
d. 3|5 – x| – 1 = 8
f. |2x| = -15