Download System Buses - St. Francis Xavier University

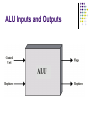
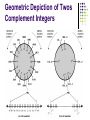
CSCI-365
Computer Organization
Lecture
Note: Some slides and/or pictures in the following are adapted from:
Computer Organization and Design, Patterson & Hennessy, ©2005
Some slides and/or pictures in the following are adapted from:
slides ©2008 UCB
Arithmetic & Logic Unit






Does the calculations
Everything else in the computer is there to
service this unit
Handles integers
May handle floating point (real) numbers
May be separate FPU (maths co-processor)
May be on chip separate FPU (486DX +)
ALU Inputs and Outputs
Binary Numerals

01101101b


Bits are numbered from the right
b7 b6b5b4b3b2b1b0
Subscripts represent the place value


bi has place value 2i
Convert to decimal

b7 * 27+b6*26 + b5*25 +b4*24 +b3*23 +b2*22 +b1*21 +
b0*20
Decimal to Binary

Decimal number is converted to binary by
repeated divisions by 2



record the remainders
Stop when you reach 0
Concatenate the remainders


The order: first remainder is least significant bit
55d = 110111b
Binary




•3 bits
1 bit
0
1
;0
;1
2 bits




00
01
10
11
;0
;1
;2
;3
•000
;0
•001
;1
•010
;2
•011
;3
•100
;4
•101
;5
•110
;6
•111
;7
4 bits and Hex

0000
;0

1000
;8

0001
;1

1001
;9

0010
;2

1010
;10 (Ah)

0011
;3

1011
;11 (Bh)

0100
;4

1100
;12 (Ch)

0101
;5

1101
;13 (Dh)

0110
;6

1110
;14 (Eh)

0111
;7

1111
;15 (Fh)
Binary to Hex




Group bits by fours (from right to left, starting with
least significant bits)
Add zeros as necessary to complete the last
group
Convert each group to the equivalent hex digit
(look up the previous table)
Ex: 0101 1110b = 5Eh
Hex to Binary



Expand each hex digit to the equivalent 4-bit
binary form
The leading zeros of leftmost digit can be
omitted
36h = 0011 0110b

(or 110110b)
Binary Storage

A pre-arranged storage size is used



typically byte, word, doubleword, or quadword
at least 8 bits will be required
encode the bits Ex: 65d is 0100 0001b
Unsigned Byte



all 8 bits used to represent the magnitude of the
number
Minimum 0 (zero) is coded as 00000000b
Maximum 255 is coded as 11111111b
Singed Byte






two’s complement code is most common
only 7 bits are used for the magnitude
Minimum -128 is coded as 10000000b
Maximum +127 is coded as 01111111b
Zero is 00000000b
Note that we can not read 10000001 as -1.
Negative Numbers


Remember -x’s 2 complement code is the same as
2n-x.
Change Sign Rule


Flip all the bits
Add 1
Geometric Depiction of Twos
Complement Integers
How Does Change Sign Rule
Come From

The 2’s Complement codes for x and -x add to a
power of 2



8-bit code: c+(-c)=28
16-bit code: c+(-c)=216
(-c)=2n-c=[(2n-1)-c]+1
=[(2n-1) + (-c)]+1


Note that (2n-1) is 1111..1b
Flip and Plus 1
Benefits



One representation of zero
Arithmetic works easily (see later)
Negating is fairly easy



3 = 00000011
Boolean complement gives
11111100
Add 1 to LSB
11111101
Two’s Compliment







+3 = 00000011
+2 = 00000010
+1 = 00000001
+0 = 00000000
-1 = 11111111
-2 = 11111110
-3 = 11111101
Can We Read 2’s Complement
Code Easily?


Positive ones: yes
00110111b(37h) --->55d
Negative ones: No!
11001001b (C9h) ---> not -49h


by Change Signed rule -55d
double check, the code should be the same as
201d ‘s code
201d = 11001001b
since -55+ 256 = 201
Conversion Between Lengths







Positive number pack with leading zeros
+18 =
00010010
+18 = 00000000 00010010
Negative numbers pack with leading ones
-18 =
11101110
-18 = 11111111 11101110
i.e. pack with MSB (sign bit)
Unsigned Addition

Numbers can be added in any number base


Use the same algorithm you practiced in second grade!
Binary Example:
c c c
10101
+ 0111
11100
Hex Addition

Hex Example:
c
c
2CF03
+435C8
704CB

A carry occurs when the sum is sixteen or
greater
Unsigned Subtraction


Borrows are worth two
sometimes you need to borrow from afar!
b b b b
-
11000011
1101001
01011010
Hex Subtraction


A borrow is worth of 16
Example:
b b
FCF03
-435C9
B993A