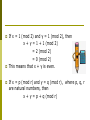* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Research in Mathematics - National Institute of Education
Ethnomathematics wikipedia , lookup
Foundations of mathematics wikipedia , lookup
List of prime numbers wikipedia , lookup
Fermat's Last Theorem wikipedia , lookup
Collatz conjecture wikipedia , lookup
System of polynomial equations wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
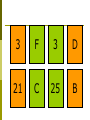
Mathematical Problems & Inquiry in Mathematics AME Tenth Anniversary Meeting May 29 2004 A/P Peter Pang Department of Mathematics and University Scholars Programme, NUS Four Important Concepts Specificity Generality Specialization Generalization D F 3 7 Each card has a number on one side and a letter on the other. Claim: “If a card has ‘D’ on one side, then it has a ‘3’ on the other.” Which cards do you need to turn over to find out if this is true? You are a bouncer in a bar. You must make sure that there are no under-age (below 21) drinkers. There are 4 customers (A—D) in the bar. You know what 2 of them are drinking and you know the age of the other 2. Customer Customer Customer Customer A is drinking beer B is drinking coke C is 25 years old D is 16 years old Which of the 4 customers do you need to check to do your job? What is a maths problem? One (possibly the most?) important aspect of inquiry in mathematics is to find a problem One important quality of a maths problem has to do with the notions of specificity and generality Consider the following problems: If x = 2 and y = 4, show that x + y = 6 If x is even and y is even, show that x + y is even Define “even” A number is even is it is two times a natural number; equivalently, an even number is divisible by 2, i.e., when divided by 2, the remainder is 0. x is even if x = 2n for some natural number n Let x = 2n and y = 2m where n and m are natural numbers x + y = 2n + 2m = 2(n+m) As n and m are natural numbers, so is n + m. This shows that x + y is even. Can this be generalized? If x is a multiple of 3 and y is a multiple of 3, then so is x + y. If x and y are multiples of p, then so is x + y. If x is odd and y is odd, is x + y odd? The number x is odd if, when divided by 2, the remainder is 1. We denote this by x = 1 (mod 2). If x = 1 (mod 2) and y = 1 (mod 2), is x + y = 1 (mod 2)? If x = 1 (mod 2) and y = 1 (mod 2), then x + y = 1 + 1 (mod 2) = 2 (mod 2) = 0 (mod 2) This means that x + y is even. If x = p (mod r) and y = q (mod r), where p, q, r are natural numbers, then x + y = p + q (mod r) Tension between Specificity and Generality Generality is often accompanied by loss of context (i.e., abstractness) D 3 F 3 D 7 21 B C 25 16 B Comparison with other disciplines Literature Science Social science A less trivial example x2 + y2 = z2 has an infinite number of positive integer solutions 2 2 x = u – v y = 2uv 2 2 z = u + v This result is believed to be due to Pythagoras What about powers higher than 2? Fermat’s Last Theorem xn + yn = zn has no integer solution when n > 2 Observation #1 (specialize to prime powers): It suffices to look at powers n that are prime Suppose there is a solution (x, y, z) for n = p x q, where p is prime. Then xpq + ypq = zpq q p q p q p (x ) + (y ) = (z ) Thus, (xq, yq, zq) would be an integer solution for the power p. Very important note: If you have a solution for the power pq, then you have a solution for the power p (and q) However, if you have a solution for the power p, it does not mean that you have a solution for the power pq (xq)p + (yq)p = (zq)p Observation #2 (specialize to “primitive solutions”) It suffices to look at solutions that are pairwise relatively prime, i.e., between any two of the three numbers x, y and z there are no common factors other than 1 For example, suppose x and y have a common factor of 2. Then, as xn + yn = zn, z will also have a factor of 2. Thus I can divide the equation through by the common factor 2. Observation #3 (generalize to rational solutions) Instead of asking for integer solutions, the problem can be equivalently stated by asking for rational solutions x = a/b y = c/d p p (a/b) + (c/d) = (e/f) z = e/f p Put the three fractions under a common denominator g (a’/g)p + (c’/g)p = (e’/g)p a’p + c’p = e’p A special case : n = 4 To show that x4 + y4 = z4 has no integer solution Strategy: Proof by contradiction Suppose there were a solution. Will show that this supposition will lead to a logical contradiction, i.e., something will go wrong. As a result, the supposition cannot be correct, and hence its opposite is correct. The solution for n = 4 uses the very interesting idea of “infinite descent” Suppose there were a solution (x, y, z), i.e., x4 + y4 = z4 Write z2 = w. Then x4 + y4 = w2 or (x2)2 + (y2)2 = w2 By Pythagoras x2 = u2 – v2, y2 = 2uv, w = u2 + v2 From this, we get x2 + u2 = v2 Again by Pythagoras, x = s2 – t2 u = 2st v = s2 + t 2 Recalling that y = 2uv, we have y2 = 2(2st)(s2 + t2) and hence Note that s, t and s2 + t2 are relatively prime. (y/2)2 = st(s2 + t2) As their product is a perfect square, so must each individual factor (s, t and s2 + t2). This means that s = x12 t = y12 s2 + t2 = w12 and hence x14 + y14 = w12 Finally, note that x1 < x y1 < y w1 < w This leads to infinite descent, which is not possible as we are dealing with positive integers. Conclusions