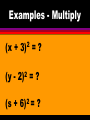* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 5
Survey
Document related concepts
Transcript
Chapter 5
Factoring
Polynomials
5-1 Factoring Integers
Factors - integers
that are multiplied
together to produce
a product.
4 x5 = 20
2,3,5,7,11,13,17,19,23,29
Prime number - is an
integer greater than
1 that has no positive
integral factor other
than itself and 1.
PRIME FACTORIZATION
Prime factorization of 36
36 = 2 x 18
=2x2x9
=2x2x3x3
2
2
=2 x3
GREATEST COMMON
FACTOR
The greatest integer
that is a factor of all
the given integers.
GREATEST COMMON
FACTOR
Find the GCF of 25 and 100
25 = 5 x 5
100 = 2 x 2 x 5 x 5
GCF = 5 x 5 = 25
5-2 Dividing
Monomials
Property of Quotients
If a, b, c and d are real
numbers, then
ac =a • c
bd b • d
Simplifying Fractions
If b, c and d are real
numbers, then
bc =c
bd d
Rule of Exponents
for Division
If a is a nonzero real
number and m and n are
positive integers, and
m > n, then am = am-n
an
Rule of Exponents
for Division
If a is a nonzero real
number and m and n are
positive integers, and
m
n > m; then a = 1
n
n-m
a
a
Rule of Exponents
for Division
If a is a nonzero real
number and m and n are
positive integers, and
m
m = n; then a = 1
an
GREATEST COMMON
FACTOR
The greatest common factor
of two or more monomials
is the common factor with
the greatest coefficient and
the greatest degree in each
variable.
GREATEST COMMON
FACTOR
Find the GCF of
50x2y5
GCF =
2
25x y
4
25x y
and
5-3
Monomial Factors of
Polynomials
Dividing a Polynomial
by a Monomial
Divide
each term of the
polynomial by the
monomial and add the
results.
Dividing Polynomials by
Monomials
5m + 35 = m + 7
5
7x2 + 14x = x + 2
7x
Factoring a Polynomial
1.
2.
3.
To factor:
Find the GCF
Divide each term by
the GCF
Write the product
Examples
2
5x
+ 10x
5
4x
–
3
6x
2
2
8a bc
–
+ 14x
2
2
12ab c
5-4 Multiplying Binomials
Mentally
When multiplying two
binomials both terms
of each binomial must
be multiplied by the
other two terms
Binomial
A
polynomial that has
two terms
2x + 3
3xy – 14
4x – 3y
613 + 39z
Trinomial
A
polynomial that has
three terms
2x2 – 3x + 1
14 + 32z – 3x
mn – m2 + n2
Multiplying binomials
Using
the F.O.I.L method
helps you remember the
steps when multiplying
F.O.I.L. Method
F
– multiply First terms
O – multiply Outer terms
I – multiply Inner terms
L – multiply Last terms
Add all terms to get
product
Example:
(2a – b)(3a + 5b)
F
– 2a · 3a
O – 2a · 5b
I – (-b) ▪ 3a
L - (-b) ▪ 5b
2
2
6a + 10ab – 3ab – 5b
6a2 + 7ab – 5b2
Example:
(x + 6)(x +4)
F
–x▪x
O – x ▪ 4
I – 6 ▪ x
L – 6 ▪ 4
x2
+ 4x + 6x + 24
x2 + 10x + 24
Section 5-5
Difference of Two
Squares
Multiplying
(x + 3) (x - 3) = ?
(y - 2)(y + 2) = ?
(s + 6)(s – 6) = ?
Factoring Pattern
2
a
–
2
b
=(a –b) (a + b)
FACTOR
2
x
- 49 = ?
16 –
2
y
=?
81t2 – 25x6 = ?
5-6 Squares of
Binomials
Examples - Multiply
(x +
(y -
2
3)
2
2)
=?
=?
(s + 6)2 = ?
Factoring Patterns
(a +
2
b)
=
2
a
+ 2ab +
2
b
(a - b)2 = a2 - 2ab + b2
•
Also known as Perfect
square trinomials
Examples – Factor
2
1. 4x
2.
3.
4.
+ 20x + 25
2
2
64u + 72uv + 81v
2
9m – 12m + 4
2
25y + 5y + 1
5-7
Factoring Pattern for
2
x + bx + c, c positive
Example
x2 + 8x + 15
Middle term is the sum of 3
and 5
Last term is the product of 3
and 5
Example
y2 + 14y + 40
Middle term is the sum of 10
and 4
Last term is the product of
10 and 4
Example
y2 – 11y + 18
Middle term is the sum of -2
and -9
Last term is the product of -2
and -9
Factor
2
1. m
– 3m + 5
2
2. k + 9k + 20
3. y2 – 9y + 8
5-8
Factoring Pattern for
2
x + bx + c, c negative
x2 - x - 20
Middle term is the sum of
4 and -5
Last term is the product of
4 and -5
Example
2
y
+ 6y - 40
Middle term is the sum of
10 and -4
Last term is the product of
10 and -4
Example
2
y
– 7y - 18
Middle term is the sum of
2 and -9
Last term is the product of
2 and -9
Factor
2
1. x
2
12k
– 4kx –
2
2. p – 32p – 33
3. a2 + 3ab – 18b2
5-9 Factoring Pattern for
ax2 + bx + c
List the factors of
• List the factors of c
• Test the possibilities to
see which produces the
correct middle term
•
2
ax
Examples
2
2x
+ 7x – 9
2
14x - 17x + 5
10 + 11x – 6x2
2
2
5a – ab – 22b
5 -10 Factor by Grouping
Factor
each polynomial
by grouping terms that
have a common factor
Then factor out the
common factor and write
the polynomial as a
product of two factors
Examples
xy – xz – 3y + 3z
3xy – 4 – 6x + 2y
xy + 3y + 2x + 6
ab – 2b + ac – 2c
9p2 – t2 – 4ts – 4s2
5 -11 Using Several Methods
of Factoring
A
polynomial is factored
completely when it is
expressed as the product
of a monomial and one or
more prime polynomials.
Guidelines for Factoring
Completely
Factor
out the greatest
monomial factor first
Factor the remaining
polynomial
Guidelines for Factoring
Completely
Make
sure that each
binomial or trinomial
factor is prime.
Example - Factor
4
-4n
+
3
40n
–
2
100n
5a3b2 + 3a4b – 2a2b3
a2bc - 4bc + a2b - 4b
5 -12 Solving Equations by
Factoring
Zero-Product Property
For all real numbers a and b:
ab = 0
if and only if
a = 0 or b = 0
Examples
1.
2.
3.
4.
(x + 2) (x – 5) = 0
5n(n – 3)(n – 4) = 0
2x2 + 5x = 12
18y3 + 8y + 24y2 = 0
5 -13 Using Factoring to
Solve Word Problems
Suppose Mike bought 36
feet of wire to make a
rectangular pen for his pet.
If he wants the area to be
80 ft2, what are the
dimensions he could use?
Solution
Let x= Length, then Width =
(36 – 2x)/2 = 18 – x
2
80 = 18x – x
x2 – 18x + 80 = 0
(x – 10) (x-8) = 0
{8, 10}
END
END
END
END
END