Download MathCAD is a versatile teaching tool

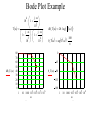
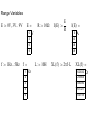
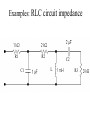
Using MathCAD
SCC Spring-08
Electronic Technology
Wang Ng
x-2638
[email protected]
Overview
•
•
•
•
•
•
•
•
About MathCAD
Using MathCAD as an interactive calculator
Using MathCAD with formulas
Equation solver
Convenient features
Advanced features
Example : AC calculations
Conclusion
General features
• MathCAD
–
–
–
–
WYSIWYG
K to 4-year College level.
Simple, easy to use.
Not intended for heavy-duty number crunching.
• MatLab
–
–
–
–
Programming style.
Up to M.S. level
Extensive training required.
Suitable for heavy-duty number crunching.
Calculator Mode
• The Calculator Tool Bar
• The “=“ key (It is the output command)
• Examples:
 1+1=2
 sin(1)=0.841
 1mi=1931m
1/3=0.333
sin(1deg)=0.017
1mi=6336ft
 Interactive: just edit the numbers
 sin(45deg)=0.707
Complex Calculations
• Use i or j for the imaginary part
 (5+3j)+(2-4j)=
 (5+3j)*(2-4j)=
 (5+3j)^2=
(5+3j)-(2-4j)=
(5+3j)/(2-4j)=
53j =
• Polar/Rectangular conversion:
 |5+3j|=
 arg(5+3j)=
 2e^45j*deg=
(type deg)
• “j” can be placed in front by typing: 1j*45deg
Formulas
• You need to provide data: use the “:” key as
the input command (it will look like :=).
• Then you need to enter the formula.
• Use the “=“ key to obtain the result.
• Example: Enter the followings




E:3V
R:2
I:E/R
I=
Equation solver
Find(x,y,...)
Solves a system of equations.
Minerr(x,y,...)
Approximate solution to a system of equations.
root(f(x),x,a,b)
Solves one equation in one unknown.
lsolve(M,v)
Solves a system of linear equations.
polyroots(v)
Solves for the roots of the polynomial whose
coefficients are in v.
This QuickSheet can be used to find a solution to the equation
f ( x)  0 for a function f(x) you specify, using the built-in root
function.
Example: Using the “root” command
Enter a function f(x):
3
x
f ( x)  x  e
Enter a guess value for the solution (modify as necessary):
x  3
soln  root ( f ( x)  x)
Note: For a complex solution, input a complex guess value.
Solution:
soln  0.773
Convenient features
• Use the worksheet as handouts.
• Specify the unit of the results.
• Change the input data and the results will be
updated automatically.
Note: Data must be placed above formulas.
•
•
•
•
Many built-in functions (root, …)
Comments can be entered after the “ key.
You can save the worksheet.
Resource center: Tutorials, quick sheets, …
Advanced features
• Symbolic process: The symbolic menu bar
– Examples: type x^2”space”-1”space” and then
select “Factor” from the symbolic menu bar.
• Graphs: see attached Bode Plot example.
• Array and range variables: Use the “;” key.
See attached example.
• Programming: The programming menu bar
has the basic programming commands.
• Calculus, differential equations, matrices,
optimization, statistics, …
Bode Plot Example
4
T  
80
70
60
50
dB_T (  ) 40
30
20
10
0

20log
j

5

10 
1  j     1  j   

3  
4 
10  
10 

dB_T   20  log  T 
_T   arg  T   

180

0
45
_T (  ) 90
135
1
1

10   1 
3
4
5
6
10 1001 10 1 10 1 10 1 10
180



0
5
10
15
20
10 1001 10 1 10 1 10 1 10

3
1
0

arg
1


180
22.5
4
5
6
Range Variables
E  0V  3V  9V
E
0 V
I ( E) 
0 A
3
0.3
6
0.6
9
0.9
f  1Hz  5Hz f 
1
R  10
E
I ( E) 
R
L  10H
Hz
XL ( f )  2f L
XL ( f ) 
62.832 
2
125.664
3
188.496
4
251.327
5
314.159
Examples: RLC circuit impedance
R1
R2
C1
C2
L
R3
f  1KHz R1  1k R2  2k R3  3k
C1  1F C2  2F L  1mH
XC1 
1
 2  f C1
XC1  159.155 
XC2 
 2  f C2
XL  6.283 
3
Z1  3  10  79.577i 
1
1
1
Z4   Z3  ( jXC1) 
Z2  0.013  6.283i
3
Z3  Z2  R2
ZTotal  Z4  R1
XL  2 f L
XC2  79.577 
Z1  R3  j XC2
1
1
Z2   Z1  ( jXL) 
1
Z3  2  10  6.283i
1
Z4  12.579  158.114i
3
ZTotal  1.013  10  158.114i
Conclusion
MathCAD is a versatile teaching tool:
• Calculation steps (formulas)
• Demonstrate specific effects
• Graphics
• Exam/Homework problems
• Partial credit
• Course note