Download Recurrence relations

R. Johnsonbaugh
Discrete Mathematics
7th edition, 2009
Instructor
Tianping Shuai
Chapter 7
Recurrence Relations
7.1 Introduction
A recurrence relation for the sequence {an} is an
equation that expresses an is terms of one or more of the
previous terms of the sequence, namely, a0, a1, …, an-1,
for all integers n with n  n0, where n0 is a nonnegative
integer.

A sequence is called a solution of a recurrence
relation if it terms satisfy the recurrence relation.

7.1 Introduction
In other words, a recurrence relation is like a
recursively defined sequence, but without specifying any
initial values (initial conditions).

Therefore, the same recurrence relation can have
(and usually has) multiple solutions.

If both the initial conditions and the recurrence
relation are specified, then the sequence is uniquely
determined.

7.1 Introduction
Example
1:
Consider the recurrence relation
an = 2an-1 – an-2 for n = 2, 3, 4, …

Is the sequence {an} with an=3n a solution of this
recurrence relation?

For n  2 we see that
2an-1 – an-2 = 2(3(n – 1)) – 3(n – 2) = 3n = an.
Therefore, {an} with an=3n is a solution of the
recurrence relation.
7.1 Introduction
Is
the sequence {an} with an=5 a solution of the same
recurrence relation?
For n  2 we see that
2an-1 – an-2 = 25 - 5 = 5 = an.
Therefore, {an} with an=5 is also a solution of the
recurrence relation.
Definition 1:A recurrence relation is an infinite
sequence a1, a2, a3,…, an,… in which the formula for
the nth term an depends on one or more preceding
terms, with a finite set of start-up values or initial
conditions
Examples of recurrence relations
Example 2:
 Initial condition a0 = 1
 Recursive formula: a n = 1 + 2a n-1 for n > 2
 First few terms are: 1, 3, 7, 15, 31, 63, …
 Example 3:
 Initial conditions a0 = 1, a1 = 2
 Recursive formula: a n = 3(a n-1 + a n-2) for n > 2
 First few terms are: 1, 2, 9, 33, 126, 477, 1809,
6858, 26001,…

Modeling with Recurrence Relations
Example:
Someone
deposits $10,000 in a savings account at a
bank yielding 5% per year with interest compounded
annually. How much money will be in the account after
30 years?
Solution:
Let
Pn denote the amount in the account after n years.
How can we determine Pn on the basis of Pn-1?
Modeling with Recurrence Relations
We
can derive the following recurrence relation:
Pn = Pn-1 + 0.05Pn-1 = 1.05Pn-1.
The initial condition is P0 = 10,000. Then we have:
P1 = 1.05P0
P2 = 1.05P1 = (1.05)2P0
P3 = 1.05P2 = (1.05)3P0
…
Pn = 1.05Pn-1 = (1.05)nP0
We now have a formula to calculate Pn for any natural
number n and can avoid the iteration.
Modeling with Recurrence Relations
Let
us use this formula to find P30 under the initial
condition P0 = 10,000:
P30 = (1.05)3010,000 = 43,219.42
After 30 years, the account contains $43,219.42.
Algorithm


1.
2.
3.
4.
5.
Input: n
Output: the account after n years
procedure interest(n)
if n =0 then
return (1000)
return(1.05 * interest(n-1))
end interest
Compound interest
Given
 P = initial amount (principal)
 n = number of years
 r = annual interest rate
 A = amount of money at the end of n years
At the end of:
 1 year:
A = P + rP
= P(1+r)
 2 years:
A = P + rP(1+r) = P(1+r)2
 3 years:
A = P + rP(1+r)2 = P(1+r)3

…

Obtain the formula A = P (1 + r) n
Modeling with Recurrence Relations
Another
example:
Let an denote the number of bit strings of length n that
do not have two consecutive 0s (“valid strings”). Find a
recurrence relation and give initial conditions for the
sequence {an}.
Solution:
Idea:
The number of valid strings equals the number of
valid strings ending with a 0 plus the number of valid
strings ending with a 1.
Modeling with Recurrence Relations
us assume that n  3, so that the string contains at
least 3 bits.
Let us further assume that we know the number an-1 of
valid strings of length (n – 1).
Then how many valid strings of length n are there, if the
string ends with a 1?
There are an-1 such strings, namely the set of valid strings
of length (n – 1) with a 1 appended to them.
Note: Whenever we append a 1 to a valid string, that
string remains valid.
Let
Modeling with Recurrence Relations
Now
we need to know: How many valid strings of
length n are there, if the string ends with a 0?
Valid strings of length n ending with a 0 must have a 1
as their (n – 1)st bit (otherwise they would end with 00
and would not be valid).
And what is the number of valid strings of length (n – 1)
that end with a 1?
We already know that there are an-1 strings of length n
that end with a 1.
Therefore, there are an-2 strings of length (n – 1) that end
with a 1.
Modeling with Recurrence Relations
So
there are an-2 valid strings of length n that end with
a 0 (all valid strings of length (n – 2) with 10 appended
to them).
As
we said before, the number of valid strings is the
number of valid strings ending with a 0 plus the
number of valid strings ending with a 1.
That
gives us the following recurrence relation:
an = an-1 + an-2
Modeling with Recurrence Relations
What
are the initial conditions?
a1 = 2 (0 and 1)
a2 = 3 (01, 10, and 11)
a3 = a2 + a1 = 3 + 2 = 5
a4 = a3 + a2 = 5 + 3 = 8
a5 = a4 + a3 = 8 + 5 = 13
…
This
sequence satisfies the same recurrence relation as
the Fibonacci sequence.
Since a1 = f2 and a2 = f3, we have an = fn+1.
Fibonacci sequence

Initial conditions:
 f1

Recursive formula:


= 1, f2 = 2
f n+1 = f n-1 + f n for n > 3
First few terms:
n
1
2
3
4
5
6
7
8
9
10
11
fn
1
2
3
5
8
13
21
34
55
89
144
Eugene Catalan

Belgian mathematician, 1814-1894
Catalan numbers are generated by the formula:
Cn = C(2n,n) / (n+1) for n > 0
 The first few Catalan numbers are:

n
0
1
2
3
4
5
6
7
8
9
10
11
Cn
1
1
2
5
14
42
132
429
1430
4862
16796
58786
Eugene Catalan

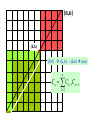
How many routes
are there from the
lower-left of n × n
square grid to the
upper-right corner
if we are restricted
to traveling only to
the right or upward
and if we are
allowed to touch
but not go above a
diagonal line from
the lower-left to the
upper-right corner?
(n,n)
(n,n)
(k,k)
(0,0)  (k, k)  (k,k)  (n,n)
n
Cn   Ck 1Cn  k
k 1
Towers of Hanoi
Start with three pegs numbered 1, 2 and 3 mounted on a
board, n disks of different sizes with holes in their
centers, placed in order of increasing size from top to
bottom.
 Object of the game: find the minimum number of
moves needed to have all n disks stacked in the same
order in peg number 3.
Rules of the game: Hanoi towers
Start with all disks stacked in peg 1 with the smallest at
the top and the largest at the bottom
 Use peg number 2 for intermediate steps
 Only a disk of smaller diameter can be placed on
top of another disk
End of game: Hanoi towers
Game ends when all disks are stacked in peg
number 3 in the same order they were stored at the
start in peg number 1.
 Verify that the minimum number of moves needed
is the Catalan number C3 = 7.
Start
End

Recurrence Relation: Hanoi towers
Cn = 2 Cn-1 +1

C1 =1
 We can prove that Cn = 2n -1

A problem in Economics
Demand equation: p = a - bq
Supply equation: p = kq
There is a time lag as supply reacts to changes in demand

Use discrete time intervals as n = 0, 1, 2, 3,…
Given the time delayed equations
pn = a – bqn (demand)
pn+1 = kqn+1 (supply)
The recurrence relation obtained is
pn+1 = a – bpn /k

Economic cobweb
with a stabilizing price
Ackermann’s function

Initial conditions:
A(0,n) = n + 1, for n = 0, 1, 2, 3,…

Recurrence relations:
A(m,0) = A(m – 1, 1), for m = 1, 2, 3,…
A(m,n) = A(m -1, A(m, n -1))
for m = 1, 2, 3,… and n = 1, 2, 3,…
7.2 Solving recurrence relations
In
general, we would prefer to have an explicit formula
to compute the value of an rather than conducting n
iterations.
For
one class of recurrence relations, we can obtain such
formulas in a systematic way.
7.2 Solving recurrence relations
Two main methods:
 Iteration
 Method for linear homogeneous recurrence relations
with constant coefficients
Method 1: Iteration

Problem: Given a recursive expression with initial
conditions a0, a1 try to express an without
dependence on previous terms.

Example: an = 2an-1 for n > 1, with initial condition
a0 = 1
 Solution: an = 2n
Method 1: Iteration
 a1 = 2

an = an-1 +3 n  2
an = an-1 +3 an-1 = an-2 +3
 an = an-1 +3= an-2 +3 +3= an-2 + 2*3
 an-2 = an-3 +3
 an = an-2 + 2*3 = an-3 +3 + 2*3 = an-3 +3 *3
 an = an-k + k*3
(let k=n-1)
 an = a1 + (n-1)*3=2 + (n-1)*3

Method 1: Iteration
Hanoi C1 = 1
 Cn = 2Cn-1 +1 n 2
Cn = 2Cn-1 +1
= 2(2Cn-2 +1)+1
= 22 Cn-2 +2+1
= 23 Cn-3 + 22 +2+1
...
= 2n-1 C1 + 2n-2 + 2n-3 + . . . + 22 +2+1
= 2n-1 + 2n-2 + 2n-3 + . . . + 22 +2+1
= 2n -1

More on the iteration method
Example: Deer Population growth
 Deer population dn at time n
 Initial condition: d0 = 1000
 Increase from time n-1 to time n is 10%.
Therefore the recursive function is
dn – dn-1 = 0.1dn-1
 dn = 1.1dn-1
 Solution: dn = 1000(1.1)n
Method 2: Linear homogeneous
recurrence relations
Definition 7.2.6 A linear homogeneous recurrence
relation of order k with constant coefficients is a
recurrence relation of the form
an = c1an-1 + c2an-2 +…+ ckan-k, ck ≠0
and initial conditions
a0 = C0, a1 = C1 , … , ak-1 = Ck-1
Method 2: Linear homogeneous
recurrence relations
The recurrence relation
Sn = 2Sn-1
is linear homogeneous recurrence relation of order 1.
The recurrence relation
fn = fn-1 +fn-2
is linear homogeneous recurrence relation of order 2.
 an =
3an-1 an-2
 an - an-1 = 2n
 an = 3n an-1
Method 2: Linear homogeneous
recurrence relations
 an =
5an-1 - 6an-2
 a0 = 7 a1 = 16
Order 2
 Solution for order 1 is of the form sn =tn 。
for example Sn = 2Sn-1
 Solution for order 2 is of the form Vn =tn ?

Method 2: Linear homogeneous
recurrence relations
Vn =tn
Vn = 5 Vn-1 - 6 Vn-2
tn = 5 tn-1 - 6 tn-2
tn - 5 tn-1 + 6 tn-2 = 0
t2 - 5 t + 6 = 0
t=2, t=3
We have two solutions
Sn = 2n Tn = 3n
Note that U n = b2n +d3n is a
solution.
To satisfy the initial conditions,
we must have
7 = U 0 = b20 +d30 =b+d
16 = U 1 = b21 +d 31 =2b+3d
b=5, d= 2
U n = 5*2n +2*3n
Method 2: Linear homogeneous
recurrence relations
Theorem 7.2.11: Given the second order linear
homogeneous recurrence relation with constant
coefficients
an = c1an-1 + c2an-2
and initial conditions a0 = C0, a1 = C1
1. If S and T are solutions then U = bS + dT is also a
solution for any real numbers b, d
2. If r is a root of t2 – c1t – c2 = 0, then the sequence
{rn}, n = 0, 1, 2,… is also a solution。
Case 1: Two different roots
3. If r1 and r2 (r1  r2) are solutions of the quadratic
equation t2 – c1t – c2 = 0, then there exist constants b
and d such that
an = br1n + dr2n
for n = 0, 1, 2, 3,…
Solving Recurrence Relations
Example:
What is the solution of the recurrence
relation an = an-1 + 2an-2 with a0 = 2 and a1 = 7 ?
Solution:
The characteristic equation of the
recurrence relation is r2 – r – 2 = 0.
Its roots are r = 2 and r = -1.
Hence, the sequence {an} is a solution to the
recurrence relation if and only if:
an = 12n + 2(-1)n for some constants 1 and 2.
Solving Recurrence Relations
the equation an = 12n + 2(-1)n and the initial
conditions a0 = 2 and a1 = 7, it follows that

a0 = 2 = 1 + 2

a1 = 7 = 12 + 2 (-1)
Solving these two equations gives us
1 = 3 and 2 = -1.
Therefore, the solution to the recurrence relation and
initial conditions is the sequence {an} with

an = 32n – (-1)n.
Given
Solving Recurrence Relations
Example:
Give an explicit formula for the Fibonacci
numbers.
Solution: The Fibonacci numbers satisfy the recurrence
relation fn = fn-1 + fn-2 with initial conditions f0 = 0 and f1 =
1.
The characteristic equation is r2 – r – 1 = 0.
Its roots are
1 5
1 5
r1 
, r2 
2
2
Solving Recurrence Relations
Therefore,
the Fibonacci numbers are given by
n
1 5 
1 5 
  2 

f n  1 



2
2




n
some constants 1 and 2.
We can determine values for these constants so that the
sequence meets the conditions f0 = 0 and f1 = 1:
f 0  1   2  0
for
1 5 
1 5 
  2
 1
f1  1 

 2 
2




Solving Recurrence Relations
The
unique solution to this system of two equations and
two variables is
1
1
1 
, 2  
5
5
So finally we obtained an explicit formula for the
Fibonacci numbers:
n
1 1 5 
1 1 5 

 


fn 
5  2 
5  2 
n
More on linear homogeneous recurrence
relations： Case 2: One root of multiplicity 2
Theorem 7.2.14: Let an = c1an-1 + c2an-2 be a second
order linear homogeneous recurrence relation with
constant coefficients.
 Let a0 = C0, a1 = C1 be the first two terms of the
sequence satisfying the recurrence relation. If r is a
root of multiplicity 2 satisfying the equation
t2 – c1t – c2 = 0,
then: there exist constants b and d such that
an = brn + dnrn
for n = 0, 1, 2, 3,…
Solving Recurrence Relations
Example:
What is the solution of the recurrence
relation an = 6an-1 – 9an-2 with a0 = 1 and a1 = 6?
Solution: The only root of r2 – 6r + 9 = 0 is r0 = 3.
Hence, the solution to the recurrence relation is
an = 13n + 2n3n for some constants 1 and 2.
To match the initial condition, we need
a0 = 1 = 1 ， a1 = 6 = 13 + 23
Solving these equations yields 1 = 1 and 2 = 1.
Consequently, the overall solution is given by
an = 3n + n3n.
Solving Recurrence Relations
dn = 4(dn - 1 - dn - 2 )
d0 = d1 =1
t2 - 4t +4 = 0
r1 = r2 = r=2
dn = b 2 n+ d n 2 n
d0 = d1 =1
d0 =1= b 2 0+ d 0 2 0 = b
d1 =1= b 2 1+ d 1 2 1 = 2 b + 2 d =1
b =1， d = - ½
dn = 2 n- n 2 n-1
Solving Recurrence Relations
For the general linear homogeneous recurrence
relation of order k with constant coefficients, if r is
a root of
tk - c1 tk-1 - c2 tk-2 - . . . - ck =0
of multiplicity m, it can be shown that
rn nrn . . . nm-1rn
are solutions.
7.3 Applications to the analysis of algorithms
1. Selection sorting
 This algorithm sorts the sequence
s1 , s2. . ., sn
in increasing order by first selecting the largest item
and placing it last and then recursively sorting the
remaining elements.
Selection Sorting Algorithm


1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Input: s1 , . . ., sn and n
Output: s1 , . . ., sn arranged in increasing order
Procedure election_sort(S,n)
// basic
if n=1 then
return
// find max
max_index :=1
for i:=2 to n do
if Si > Smax_index then
max_index :=i
//move
swap(si, Smax_index)
call election_sort(S,n-1)
end election_sort
Selection Sorting Algorithm
bn ,：the number of comparisons.
The initial condition b1 =0
bn = n-1+ bn-1
Line bn
= bn-1 + n-1
1-7 ： 0
= (bn-2 + n-2) + n-1
8 ： n-1
= (bn-3 + n-3) + n-2 + n-1
9-11: 0
= b1 +1+2+3+ . . . +(n-1)
12: bn-1
= 0+ 1+2+3+ . . . +(n-1)
2)
=
(n-1)*n/2=
(n
b = n-1+ b
n
n-1
Review
1. Selection sorting
a) Given a sequence of n terms ak, k = 1, 2,…, n to
be arranged in increasing order
b) Count the number of comparisons bn with initial
condition b1 = 0
c) Obtain recursion relation bn = n – 1 + bn-1 for n =
1, 2, 3,…
d) bn = n(n-1)/2 = (n2)
Binary search
Input: si , si+1. . ., sj , i 1 and key, i, j
Output: sk=key, k; not found, 0
1.
Procedure binary_search(s,i,j,key)
2.
if i > j then
3.
return(0)
4.
k=  (i+j)/2 
5.
if key = Sk then
6.
return(k)
7.
if key< Sk then
8.
j:= k-1
9.
else
10.
i:=k+1
11.
return(binary_search(s,i,j,key))
12.
end binary_search
Binary search

Let an denote the worst-case time.
n=1, i=j, key not found, a1 =2
n>1, an =1+a n / 2 
an =1+a n / 2  If n=2k , then
a2k =1+ a2k-1
Let bk =a2k , we obtain
bk = 1+ bk-1 , b0 = a1 =2
bk = 1+ bk-1 = 2+ bk-2 = . . . =k+ b0 =k+ 2
Thus, if n=2k,
an = lg n+ 2
Binary search
An arbitrary value of n falls between two powers of 2,
say
a2k -1 < an  a2k
Notice that
k-1 < lgn  k
We deduce
lgn < k+1= a2k-1  an  a2k
=k+ 2 <3 + lgn=O(lgn)
an =  (lgn)
Review
2. Binary search
Problem: Search for a value in an increasing
sequence. Return the index of the value, or 0 if
not found.
 Initial condition a1 = 2
 Recurrence relation an = 1 + an/2
 Result: an = (lg n)
Theorem 7.3.4: The worst-case time for binary
search for input is  (lgn)
7.3 Applications to the analysis of algorithms
1. Selection sorting  (n2 )
2. Binary search  (nlgn)
3. Merge sort  (nlgn)
Merging two sequences
Problem: Combine two increasing sequences into a
single increasing sequence (merge two sequences).
Si ， . . . , Sj
Si ， . . . , Sm Sm+1 ， . . . , Sj
m= (i+j)/2
Merging two sequences
Input: Two increasing sequences:
Si ， . . . , Sm and
Sm+1 ， . . . , Sj，and index i, j, m
 Output: increasing sequences
ci ， . . . , cj

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
Procedure merge(s,i,m,j,c)
// p -> Si ， . . . , Sm
// q -> Sm+1 ， . . . , Sj
// r -> ci ， . . . , cj
p:=i
q:=m+1
r := i
//
while p <= m and q <=j do
begin
if Sp < Sq
begin
cr := Sp
p ：=p+1
end
else
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
begin
cr := Sq
q ：=q+1
end
r:=r+1
end
// copy the rest elements in the 1st sequence
while p <= m do
begin
cr := Sp
p ：=p+1
r:= r+1
end
// copy the rest elements in the 2nd sequence
while q <= j do
begin
cr := Sq
q ：=q+1
r:= r+1
end
End merge
Merging two sequences

Theorem 7.3.7: To merge two sequences
the sum of whose lengths is n, the number
of comparisons required is n-1.
Merge sort algorithm


1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Input: Si ， . . . , Sj i, j
Output: increasing sequences Si ， . . . , Sj
procedure merge_sort(s, i, j)
//i=j
ifi=j then
return
//分解
m:= m= (i+j)/2
call merge_sort(s, i , m)
call merge_sort(s, m+1, j)
// merge
call merge(s,i,m,j,c)
//copy
for k:=i to j do
Sk := Ck
end merge_sort
Merge sort

12, 30, 21, 8, 6, 9, 1, 7

12 30

8 12 21 30

8 21
69
17
1679
1 6 7 8 9 12 21 30
n=2k
a2k =2a2k-1 + 2 k - 1
a2k = 2a2k-1 + 2 k - 1
= 2(2a2k-2 + 2 k-1 - 1) + 2 k - 1
= 22 a2k-2 + 2*2 k - 1-2
= 23 a2k-3 + 3*2 k - 1-2- 22
=...
=2k a20 + k*2 k - 1-2- 22 - . . .- 2k-1
= k*2 k - (2 k - 1)
= (k-1) 2 k +1
a2k -1  an  a2k
k-1 < lgn  k
 (nlgn)=(-2+lgn)*n/2<(k-2) 2k-1 +1
=a2k -1  an  a2k
 k2k+1  (1+lgn)*2n +1
=O(nlgn)
an =  (nlgn)
Theorem 7.3.10: The merge sort algorithm is (n lg n)
in the worst case.