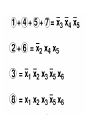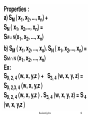Download Boolean Algebra

BOOLEAN ALGEBRA
Boolean Algebra
1
BOOLEAN ALGEBRA
-REVIEW
Boolean Algebra was proposed by George Boole in 1853.
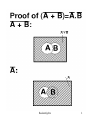
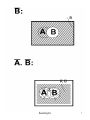
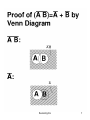
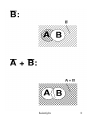
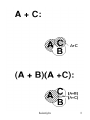
Basically AND,OR NOT can be expressed as Venn Diagrams
Boolean Algebra
2
Boolean Algebra
3
Boolean Algebra
4
Boolean Algebra
5
Boolean Algebra
6
Boolean Algebra
7
Boolean Algebra
8
Boolean Algebra
9
Boolean Algebra
10
Boolean Algebra
11
Boolean Algebra
12
Boolean Algebra
13
Boolean Algebra
14
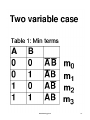
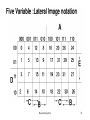
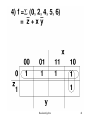
Min Terms and Max Terms
Min Terms are those which occupy
minimum area on Venn Diagram
Max Terms are those which occupy
maximum area on Venn diagram.
Boolean Algebra
15
Boolean Algebra
16
Boolean Algebra
17
Boolean Algebra
18
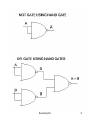
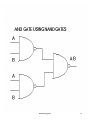
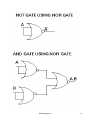
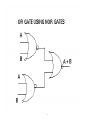
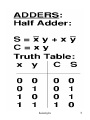
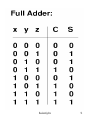
LOGIC GATES
Nand and Nor gates are called Universal gates
as any Boolean function can be realized with the
help of Nand and Nor gates only
Boolean Algebra
19
For example, NOT, OR, AND gates can be realized
by only Nand gates.
Boolean Algebra
20
Boolean Algebra
21
Boolean Algebra
22
Boolean Algebra
23
Boolean Algebra
24
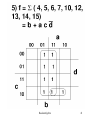
SIMPLIFICATION OF
BOOLEAN FUNCTIONS
•
•
•
•
Algebraic Method
Tabular Method
K-Map Method
Schienman Method
Boolean Algebra
25
ALGEBRAIC METHOD
Simplify using algebraic theorems
Advantage:
First Method based on Boolean Algebra theorems
Disadvantage:
No Suitable algorithm to apply (Trial type of method)
Boolean Algebra
26
TABULAR METHOD
Also called Quine McClusky Method
Advantage:
It may work for any no. of variables
Disadvantage:
Simplification from table is quite involved
Boolean Algebra
27
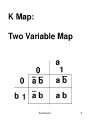
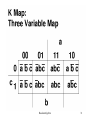
K-MAP METHOD
Karnaugh Map. Also called Vietch
Karnaugh Method.
Advantage:
Simplest and Widely accepted
Disadvantage:
Applicable for only upto Six variables
Boolean Algebra
28
SCHIENMAN METHOD
Columnwise writing of minterms as
decimal numbers and their simplification
Advantage:
Very suitable for computerization. Applicable for any
number of variables. Parallel Processing
Disadvantage:
May not result in most simplified answer for some
problems
Boolean Algebra
29
Boolean Algebra
30
Boolean Algebra
31
Boolean Algebra
32
Boolean Algebra
33
Boolean Algebra
34
Boolean Algebra
35
Boolean Algebra
36
Boolean Algebra
37
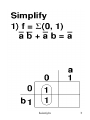
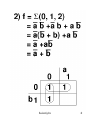
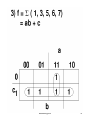
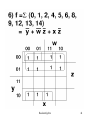
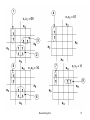
Steps for simplification:
• Try to find single one’s
– 2 one’s
– 4 one’s
– 8 one’s
Always see is a higher combination exists. If a
higher combination exists, wait. Be sure that
you have managed the lower combination first.
Boolean Algebra
38
Boolean Algebra
39
Boolean Algebra
40
Boolean Algebra
41
Boolean Algebra
42
Boolean Algebra
43
Boolean Algebra
44
Boolean Algebra
45
Boolean Algebra
46
Boolean Algebra
47
Boolean Algebra
48
Boolean Algebra
49
Boolean Algebra
50
Boolean Algebra
51
Boolean Algebra
52
Boolean Algebra
53
Boolean Algebra
54
Boolean Algebra
55
Boolean Algebra
56
Boolean Algebra
57
Boolean Algebra
58
SYMMETRIC FUNCTIONS
• DEFINITION
• PROPERTIES
• IDENTIFICATION
Boolean Algebra
59
Definition
A switching function of n variables
f(X1,X2….Xn) is called a symmetric (or
totally symmetric), if and only if it is invariant
under any permutation of its variables. It is
partially symmetric in the variables Xi,Xj
where {Xi,Xj} is a subset of {X1,X2…Xn} if
and only if the interchange of the variables
Xi,Xj leaves the function
unchanged.
Boolean Algebra
60
EXAMPLES
• f(x,y,z) = x’y’z+xy’z’+x’yz’
If we substitute x = y and y = x
x = z and z = x
y = z and z = y
TOTALLY SYMMETRIC with respect to x,y,z
• f(x,y,z) = x’y’z + xy’z’
is Prettily Symmetric in the variables x and z.
(x = z and z = x)
• f(x,y,z) = z’y’x + zy’x’
is a Symmetric function
(x = y and y = x)Boolean Algebra
61
• f(x,y,z) = y’x’z +yx’z’)
is Not a Symmetric function
This function is symmetric w.r.t x and z, but not symmetric
w.r.t x and y. So Partially Symmetric
•f(x1,x2,x3) = x1’x2’x3’ + x1x2’x3+ x1’x2x3
is not symmetric w.r.t. the variables x1,x2,x3, but is
symmetric w.r.t the variables x1,x2,x3’
>> f is not invariant under an interchange of variables
x1,x3.
That is, x3’x2’x1’+x3x2’x1 +x3’x2x1 != f
>> But f is invariant under an interchange of variables
x1,x3’
That is, x3x2’x1 + x3’x2’x1 + x3x2x1’ = f
So f is symmetric w.r.t the variables x1,x2 and x3’
Boolean Algebra
62
The variables in which a function is
symmetric are called the
VARIABLES OF SYMMETRY
Boolean Algebra
63
Necessary and Sufficient condition for
function f(x1,x2….xn) to be symmetric is that
it may be specified by a set of numbers
{a1,a2…ak} where 0<an<n,such that it
assumes the value 1 when and only when ai of
the variables are equal to 1. The numbers in
the set are called the a-numbers
Boolean Algebra
64
A Symmetric function is denoted by
Sa1,a2…ak (x1,x2….xn), where S designates the
property of symmetry, the subscripts designate
the a numbers, and (x1,x2….xn) designate the
variables of symmetry.
Boolean Algebra
65
Boolean Algebra
66
Boolean Algebra
67
Boolean Algebra
68
Boolean Algebra
69
IDENTIFICATION
The switching function to be tested for
symmetry is written as a table in which all the
minterms contained in the function are listed
by their binary representation
Boolean Algebra
70
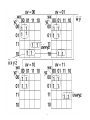
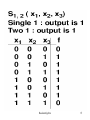
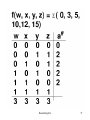
For example, the function f(x,y,z) =
(1,2,4,7) is written as shown:
x y z a#
The arithmetic sum of each
0 0 1 1
column in the table is computed
0 1 0 1
written under the column. This
1 0 0 1
sum is referred to as a column1 1 1 3
sum. The number of 1’s in each
2 2 2
row is written in the corresp.
position in column a#. This no. is called
ROW SUM.
Boolean Algebra
71
If an n-variable function is symmetric and one
of its row sums is equal to some number a, then,
by definition, there must exist n!/(n-a)!a! rows
which have the same row sum.
If all the rows occur the required number of times,
then all colums sums are identical
Boolean Algebra
72
For the example, all column sums equal 2,
and there are two row sums, 1 and 3, that must
be checked for “Sufficient Occurrence”.
>> 3!/(3-1)! = 3 ; 3!/(3-3)! = 1
Both row sums occur the required number of
times. Therefore, the function is symmetric
and can be expressed by S1,3(x,y,z).
Boolean Algebra
73
Boolean Algebra
74
The column sums are 6 4 4 6
Since the column sums are not all the same,
further tests must be performed to determine
if the function is symmetric, and if it is, to
find its variables of symmetry.
The column sums can be made the same by
complementing the columns corresponding
to variables x and y.
Boolean Algebra
75
Boolean Algebra
76
The new column sums are now computed and are
found identical. The row sums are determined
next and entered as a#. Each row sum is tested
by the binomial co-efficient occurrence.
4!/(4-2)! = 6 ; 4! /(4-3)!3! = 4
Since, all row sums occur the required number
of times, the function is symmetric,its variables
of summetry are w,x’,y’,z and its a numbers are 2
and 3. ( f = S2,3(w,x’,y’,z))
Boolean Algebra
77
If columns w and z are complimented, instead
of x and y, the table shown below results and \
since all its row sums occur the required no. of
times, f can be written as f = S1,2(w’,x,y,z’)
Boolean Algebra
78
Boolean Algebra
79
The column sums are all identical, but row
sum 2 does not occur six times as required.
One way to overcome this difficulty is by
expanding the function about any one of its
variables
Boolean Algebra
80
The function can be expanded about w.
w x y z
0 0 0 0
0 0 1 1
0 1 0 1
a#
0
2
2
Column Sums :
x y z
1 1 2
The column sums can be made by complementing
the columns corresponding to variables x and y.
Boolean Algebra
81
x’
1
1
0
y’
1
0
1
z a#
0 2
1 2
1 2
Column Sums:
x y z
2 2 2
Each row is tested by the binomial coefficients
for sufficient occurrence.
3!/(3-2)!2! = 3
Symmetry: S2(x’,y’,z)
Boolean Algebra
82
w x y z
1 0 1 0
1 1 0 0
1 1 1 1
2 2 1
x
0
1
1
2
y
1
0
1
2
z’
1
1
0
2
a#
1
1
3
a#
2
2
2
The column sums can be made
the same by complementing
the columns corresponding
to variable z.
Each row is tested by the
binomial coefficients for
sufficient occurrence.
Boolean Algebra
83
3!/(3-2)! 2! = 3
Symmetry:
S2(x,y,z’)
So the function f is written as
f=w’S2(x’,y’,z) + wS2(x,y,z’)
Boolean Algebra
84
questions?
Boolean Algebra
85