Download 11_1 Square Roots and Irrational Numbers

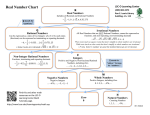
Start
Bellwork #
Chapter 11-1 p.560
Square Roots
and
Irrational
Numbers
3
2
1
12  1
22  4
32  9
The square of an integer is a
perfect square.
The opposite of squaring a
number is taking the square root.
Example

For example 81
asks what number multiplied by itself is equal
to 81? That number is 9.
Is there another solution to that problem?
Example

For example 81
asks what number multiplied by itself is equal
to 81? That number is 9.
Is there another solution to that problem?
Yes, -9 is also a solution.
Simplify each square root
100
 16
Simplify each square root
100
 16
10
Simplify each square root
100
10
 16
-4
Squares and roots

Here is a list that will be helpful:
12  1
1 1
22  4
4 2
32  9
9 3
42  16
16  4
52  25
25  5
62  36
36  6
7 2  49
49  7
82  64
64  8
92  81
81  9
102  100
100  10
112  121
121  11
122  144
144  12

Do you see that squares and square
roots are inverses (opposites) of each
other?
Estimating square roots

Once we have memorized these
squares and their roots, we can
estimate square roots that are not
perfect squares

For example, what about
8
?
Estimating square roots



We find the two perfect squares that are before
and after the square root of 8. . .
4 and 9
Look at them on a number line:
2
3
4
2
5
6
7
8
9
3
Estimating square roots

8 is between 2 and 3 but
We can see that
is closer to 3. We would say that 8 is
approximately 3.
2
3
4
2
5
6
7
8
9
3
TRY THIS:
Estimate to the nearest whole number
27
 78
50
TRY THIS:
Estimate to the nearest whole number
27
 78
50
5
TRY THIS:
Estimate to the nearest whole number
27
 78
50
5
-9
TRY THIS:
Estimate to the nearest whole number
27
5
 78
-9
50
7

Rational number- can be written as
a fraction

Irrational number- cannot be written
as a fraction because:
• it is a non-terminating decimal
• it is a decimal that does NOT repeat
* The square roots of ALL perfect
squares are rational.
* The square roots of numbers that are
NOT perfect squares are irrational.
Try This: Identify each number as
rational or irrational
2
 81
0.53
0.627
13.875931...
Try This: Identify each number as
rational or irrational
2
 81
0.53
0.627
13.875931...
Irrational
Try This: Identify each number as
rational or irrational
2
 81
0.53
0.627
13.875931...
Irrational
Rational
Try This: Identify each number as
rational or irrational
2
Irrational
 81
Rational
0.53
Rational
0.627
13.875931...
Try This: Identify each number as
rational or irrational
2
Irrational
 81
Rational
0.53
Rational
0.627
Rational
13.875931...
Try This: Identify each number as
rational or irrational
2
Irrational
 81
Rational
0.53
Rational
0.627
Rational
13.875931...
Irrational
Agenda
PA#48
P.562
Print
#16-35
out CAT 6 review from
my website or
teacherweb.com (P.9-30)