Download structures - UBC Computer Science

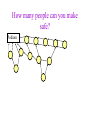
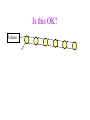
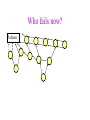
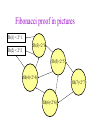
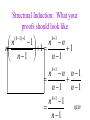
CS121
Induction
Alan J. Hu
1
Induction: The Big Picture
•
•
We’ll develop your intuition about induction.
We’ll see examples of weak, strong, and
structural induction.
Two different learning goals:
1. Learning the CONCEPT of induction.
2. Learning the FORM of an induction proof.
•
We’ll see why they are really all the same.
A Little Game
Are you all willing to stand up and move around the
classroom?
(If not, I can still convey the ideas, but it won’t be as
memorable.)
A Little Game
Everyone in this room fails CPSC 121, unless…
A Little Game
Everyone in this room fails CPSC 121, unless…
you make yourself “safe” by following these
rules:
1. The podium at the front of class is safe.
2. Anyone who puts both hands on something or
someone safe is also safe.
(3. There is no other way to be safe.)
How do you make everyone safe?
Podium
Do you have to fight for the podium?
Podium
You can be good Canadians…
Podium
You can be less structured…
Podium
How many people can you make
safe?
Podium
Is this OK?
Podium
Or worse, this?
Podium
Who fails now?
Podium
Who fails here?
Podium
What’s the point?
• This is exactly how induction works in general!
• Base Case: Some cases where you know the
property holds already.
• Inductive Case: You must show that the property
holds for any given item, by showing how it is
implied by the property on items closer to the base
case.
• If you can show the inductive case for all elements in
a set, the property holds for all of them – even an
infinite number!
What’s the point?
•
•
•
•
This is exactly how induction works in general!
If anyone breaks the chain, the proof fails.
If anyone misses the base case, the proof fails.
If there are any cycles (rather than getting closer
to base case), the proof fails.
On the other hand, if you get induction right, it’s a
very easy and powerful way to write a proof!
Weak Induction
•
•
•
•
This is what you are usually taught first.
Goal: Prove p(n) for all natural numbers n
Base Case: Prove p(0) (and maybe p(1), etc.)
Inductive Case: Assume p(k) for some arbitrary k
and prove that it implies p(k+1).
Weak Induction: What’s really
happening?
•
•
•
•
This is what you are usually taught first.
Goal: Prove p(n) for all natural numbers n
Base Case: Prove p(0) (and maybe p(1), etc.)
Inductive Case: Assume p(k) for some arbitrary k
and prove that it implies p(k+1).
This is just the polite Canadians version of the game!
p(x) just means x is safe. Base case is the podium.
Inductive case says that an arbitrary p(k) is true
because he’s got both hands on p(k-1), who is
closer to the base case.
Weak Induction: What your proof
should look like
Problem: Prove that the solution to the n disk
Towers of Hanoi takes 2^n-1 moves.
(Aside: Do you know this problem?)
Weak Induction: What your proof
should look like
Problem: Prove that the solution to the n disk
Towers of Hanoi takes 2^n-1 moves.
Proof: The proof is by induction on n.
Base Case: n=0. In this case, 0 moves are required.
2^0 – 1 = 0, so the property holds on the base
case.
Weak Induction: What your proof
should look like
Problem: Prove that the solution to the n disk Towers of
Hanoi takes 2^n-1 moves.
Proof: The proof is by induction on n.
Inductive Case: The inductive assumption is that moving a
stack of n-1 disks takes 2^(n-1) – 1 moves. Moving a
stack of n disks means moving n-1 disks to the
intermediate stack, moving the nth disk from start to
destination, and the moving the n-1 disks from the
intermediate stack to the destination. (continued)
Weak Induction: What your proof
should look like
Problem: Prove that the solution to the n disk
Towers of Hanoi takes 2^n-1 moves.
Proof: The proof is by induction on n.
Inductive Case: (continued) Using the inductive
assumption, the total number of moves is 2^(n-1)
– 1 + 1 + 2^(n-1) – 1 which simplifies to 2^n – 1.
QED
Weak Induction: What your proof
should look like
Problem: Prove that the solution to the n disk
Towers of Hanoi takes 2^n-1 moves.
Proof: The proof is by induction on n.
Inductive Case: (continued) Using the inductive
assumption, the total number of moves is 2^(n-1)
– 1 + 1 + 2^(n-1) – 1 which simplifies to 2^n – 1.
QED
(Aside: This is usually taught as assuming n and
proving n+1, which is OK, too.)
Strong Induction
•
•
•
•
This is often taught as something special…
Goal: Prove p(n) for all natural numbers n
Base Case: Prove p(0) (and maybe p(1), etc.)
Inductive Case: Assume p(0) through p(k) for
some arbitrary k and prove that it implies p(k+1).
Strong Induction: What’s Really
Happening
•
•
•
•
This is often taught as something special…
Goal: Prove p(n) for all natural numbers n
Base Case: Prove p(0) (and maybe p(1), etc.)
Inductive Case: Assume p(0) through p(k) for
some arbitrary k and prove that it implies p(k+1).
This is just the unstructured version of the game!
As long as p(k+1) has as many hands as the rules
require on p(0)…p(k) (who are closer to base
case), the property holds.
Strong Induction: What your proof
should look like
Problem: Prove that the nth Fibonacci number is
less than 2^n.
(Aside: Do you know this problem?)
Strong Induction: What your proof
should look like
Problem: Prove that the nth Fibonacci number is
less than 2^n.
Proof: The proof is by (strong) induction on n.
Base Case: When n=1, the 1st Fibonacci number is
1, which is less than 2, which is 2^1. When n=2,
the 2nd Fibonacci number is also 1, which is less
than 4, which is 2^2. So the base cases hold.
Strong Induction: What your proof
should look like
Problem: Prove that the nth Fibonacci number is less than
2^n.
Proof: The proof is by (strong) induction on n.
Inductive Case: For all n>2, the nth Fibonacci number is
defined to be fib(n-1)+fib(n-2). By the inductive
assumption, fib(n-1) < 2^(n-1) and fib(n-2) < 2^(n-2).
Therefore, fib(n) = fib(n-1) + fib(n-2) < 2^(n-1) + 2^(n-2)
< 2^(n-1) + 2^(n-1) = 2^n. QED
Fibonacci proof in pictures
fib(1) < 2^1
fib(3)<2^3
fib(2) < 2^2
fib(5)<2^5
fib(4)<2^4)
fib(7)<2^7
fib(6)<2^6)
Strong Induction: What went
wrong?
Theorem: All horses are the same colour.
Proof: By (strong) induction on n, the number of horses in
any set of horses.
Base Case: n=1. 1 horse is the same colour as itself.
Inductive Case: Assume all sets of horses of size from 1 to n1 are the same colour. Given any set of horses of size n,
separate one from the herd. Call this horse A. By the
inductive assumption, the remaining n-1 horses are the
same colour. Now, put back the first horse and separate
out a different horse, called B; similarly, the remaining n-1
horses are the same colour.
Strong Induction: What went
wrong?
Theorem: All horses are the same colour.
Proof: By (strong) induction on n, the number of horses in
any set of horses.
Base Case: n=1. 1 horse is the same colour as itself.
Inductive Case: (continued) But, those two sets of n-1 horses
had n-2 horses in common, and horses don’t change
colour! So A has the same colour as the n-2, who have the
same colour as B. So, they all must be the same colour, by
transitivity of equality. QED
Structural Induction
• This is extremely common in computer science!
• Goal: Prove p(n) for all structures n.
(Aside: This only works when the set of all possible
structures is defined recursively/inductively.)
• Base Case: Prove p for all the base case structures.
• Inductive Case: For an arbitrary non-base-case
structure n, show that p(n) holding on the structure is
implied by p holding on the sub-structures.
Structural Induction: What’s Really
Happening
• This is extremely common in computer science!
• Goal: Prove p(n) for all structures n.
(Aside: This only works when the set of all possible
structures is defined recursively/inductively.)
• Base Case: Prove p for all the base case structures.
• Inductive Case: For an arbitrary non-base-case
structure n, show that p(n) holding on the structure is
implied by p holding on the sub-structures.
This is still the same game!
Structural Induction: What your
proofs should look like
Problem: Prove that a perfect/complete n-ary tree of height h
has (n^(h+1) – 1)/(n – 1) nodes.
Aside: Do you know what a tree is yet?
A tree is either a leaf (a node with no children), or a node
whose children are trees.
In an n-ary tree, the each non-leaf node has n children.
In a perfect/complete tree, all leaves are at the same depth.
Structural Induction: What your
proofs should look like
Problem: Prove that a perfect/complete n-ary tree of height h
has (n^(h+1) – 1)/(n – 1) nodes.
Aside: Do you know what a tree is yet?
A tree is either a leaf (a node with no children), or a node
whose children are trees.
In an n-ary tree, the each non-leaf node has n children.
In a perfect/complete tree, all leaves are at the same depth.
Structural Induction: What your
proofs should look like
Problem: Prove that a perfect/complete n-ary tree of
height h has (n^(h+1) – 1)/(n – 1) nodes.
Proof: The proof is a structural induction on trees.
Base Case: If the tree is a single leaf, then it has
height 0 and 1 node. The formula evaluates as
(n^(0+1) – 1)/(n – 1) = 1.
Structural Induction: What your
proofs should look like
Problem: Prove that a perfect/complete n-ary tree of
height h has (n^(h+1) – 1)/(n – 1) nodes.
Proof: The proof is a structural induction on trees.
Inductive Case: If the tree is not a leaf, then it must
have n children (because it is n-ary), each of
which is a tree. Because it is perfect/complete, the
height of each of these subtrees is h-1.
(continued)
Structural Induction: What your
proofs should look like
Problem: Prove that a perfect/complete n-ary tree of
height h has (n^(h+1) – 1)/(n – 1) nodes.
Proof: The proof is a structural induction on trees.
Inductive Case: (continued) By the inductive
hypothesis, each of those trees, therefore, have
(n^((h-1)+1) – 1)/(n – 1) nodes. Adding up all the
nodes, we have n times the above, plus 1 for the
root. Simplifying the math, we have…
Structural Induction: What your
proofs should look like
n
1 
n n
  1 
n
1
n 1
 n 1 
h 1
n  n n 1


n 1
n 1
h 1
n 1
QED!

n 1
( h 1) 1
h 1
Induction Is Induction
• Weak, strong, and structural induction get taught
as if they were separate concepts, but they are all
the same. We will see:
– Weak and strong induction are the same.
– Weak is a special case of structural induction.
Weak Induction = Strong Induction
• We are trying to prove some property P(n) for all
natural numbers n.
• Base cases are the same: Prove P(0) or other small
cases.
• In weak induction, we get to assume P(k-1) to prove
P(k).
• In strong induction, we get to assume P(0) through
P(k-1) to prove P(k).
• So, clearly, every weak induction proof is a strong
induction proof. What about the other way around?
Weak Induction = Strong Induction
• We are trying to prove some property P(n) for all
natural numbers n.
But we have no limitations on what P(n) is!
• Given a strong induction proof for P(n), define Q(n)
to be the property:
Q(n) = “P(k) holds for all 0<=k<n”
• The strong induction proof of P(n) becomes a weak
induction proof on Q(n).
Weak Induction Is Structural
Induction
• Weak induction proves p(n) for all natural numbers.
• Structural induction proves p(n) for all structures n,
which are defined inductively.
What are natural numbers, really?
Peano Postulates/Axioms
• By Giuseppe Peano, in 1889.
• This is the formal way mathematicians define
natural numbers.
Peano Postulates/Axioms
1. 0 is a natural number.
2. For every natural number n, S(n) is a natural
number.
3. For every natural number n, S(n)!=0.
4. For all natural numbers m and n, if S(m)=S(n),
then m=n.
5. If K is any set that obeys #1 and #2, then K
contains all natural numbers.
Peano Postulates/Axioms
Natural numbers are defined inductively!
1. 0 is a natural number.
2. For every natural number n, S(n) is a natural
number.
3. For every natural number n, S(n)!=0.
4. For all natural numbers m and n, if S(m)=S(n),
then m=n.
5. If K is any set that obeys #1 and #2, then K
contains all natural numbers.
Peano Postulates/Axioms
1. 0 is a natural number.
2. For every natural number n, S(n) is a natural
number.
3. For every natural number n, S(n)!=0.
4. For all natural numbers m and n, if S(m)=S(n),
then m=n.
5. If K is any set that obeys #1 and #2, then K
contains all natural numbers.
Nothing else is a natural number. (So, if you do the structural
induction, you’ve proven your result for all n.)
Weak Induction Is Structural
Induction
Weak induction is just structural induction on the
natural numbers (as they are formally defined).
Base Case: Prove the property for p(0).
Inductive Case: Any non-base-case number is of the
form S(k) for some k. By the inductive
hypothesis, p(k) holds. Use this fact to prove
p(S(k)).