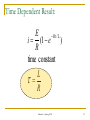* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Time Varying Circuits
Electrical substation wikipedia , lookup
Power engineering wikipedia , lookup
Stray voltage wikipedia , lookup
Electrical ballast wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Three-phase electric power wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Opto-isolator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electric machine wikipedia , lookup
Current source wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Mains electricity wikipedia , lookup
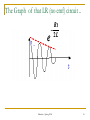
Buck converter wikipedia , lookup
Rectiverter wikipedia , lookup
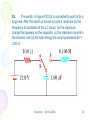
Time Varying Circuits 2006 Induction - Spring 2006 1 What is going on? There are only 7 more classes and the final is 3 weeks away. Exam Issues Scotty, beam me somewhere else! Look Ashamed! Inductor Circuits Quiz Friday AC Next week & Following Monday Induction - Spring 2006 2 Other Wire Second Problem B q h q a Both Currents are going into the page. B total a 0 2 B Sin (q ) 2 I Sin (q ) 2r Sin (q ) 1 h h B~ ~ ~ r r r a2 h2 d h( 2h) a 2 h 2 B~ 0(max) dh stuff Induction - Spring 2006 h a 3 First Problem DV 1 2 qDV mv 2 mv2 qvB R 2qDV v m qBR qBR m m v 2qDV q 2 B 2 R 2 qB 2 R 2 m eR 2 (const ) 2qDV 2DV M 2e(2 R) 2 8eR 2 M /m8 Induction - Spring 2006 4 The Last two Problems were similar to WebAssigns that were also reviewed in class. Circular Arc – Easy Biot-Savart Moving Rod Induction - Spring 2006 5 Question What about these problems was “unfair”? Why so many blank or completely wrong pages? Induction - Spring 2006 6 And Now ….. From the past Induction - Spring 2006 7 Max Current Rate of increase = max emf VR=iR ~current Induction - Spring 2006 8 E (1 e Rt / L ) R L (time constant) R i Induction - Spring 2006 9 We also showed that 1 2 uinductor B 20 1 2 ucapacitor 0 E 2 Induction - Spring 2006 10 LR Circuit i Steady Source sum of voltage drops 0 : di E iR L 0 dt same form as the capacitor equation q dq E R 0 C dt Let E 0, then Induction - Spring 2006 11 Time Dependent Result: E Rt / L i (1 e ) R time constant L R Induction - Spring 2006 12 R L Induction - Spring 2006 13 At t=0, the charged capacitor is now connected to the inductor. What would you expect to happen?? Induction - Spring 2006 14 The math … For an RLC circuit with no driving potential (AC or DC source): Q di L 0 C dt dQ Q d 2Q R L 2 0 dt C dt Solution : iR Q Qmax e Rt 2L cos(d t ) where 1 R d LC 2 L Induction - Spring 2006 2 1/ 2 15 The Graph of that LR (no emf) circuit .. e Rt 2L Induction - Spring 2006 16 Induction - Spring 2006 17 Mass on a Spring Result Energy will swap back and forth. Add friction Oscillation will slow down Not a perfect analogy Induction - Spring 2006 18 Induction - Spring 2006 19 LC Circuit Low High Q/C High Low Induction - Spring 2006 20 The Math Solution (R=0): LC Induction - Spring 2006 21 New Feature of Circuits with L and C These circuits produce oscillations in the currents and voltages Without a resistance, the oscillations would continue in an un-driven circuit. With resistance, the current would eventually die out. Induction - Spring 2006 22 Variable Emf Applied 1.5 1 Volts emf 0.5 DC 0 0 1 2 3 4 5 6 7 8 9 10 -0.5 -1 Sinusoidal -1.5 Tim e Induction - Spring 2006 23 Sinusoidal Stuff emf A sin( t ) “Angle” Phase Angle Induction - Spring 2006 24 Same Frequency with PHASE SHIFT Induction - Spring 2006 25 Different Frequencies Induction - Spring 2006 26 Note – Power is delivered to our homes as an oscillating source (AC) Induction - Spring 2006 27 Producing AC Generator xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx xxxxxxxxxxxxxxxxxxxxxxx Induction - Spring 2006 28 The Real World Induction - Spring 2006 29 A Induction - Spring 2006 30 Induction - Spring 2006 31 The Flux: B A BA cos t emf BA sin t emf i A sin t Rbulb Induction - Spring 2006 32 April 12, 2006 Induction - Spring 2006 33 Schedule Today Friday Quiz on this weeks material Some problems and then AC circuits Monday Finish Inductors Last FULL week of classes Following Monday is last day of class FINAL IS LOOMING! Induction - Spring 2006 34 Some Problems Induction - Spring 2006 35 14. Calculate the resistance in an RL circuit in which L = 2.50 H and the current increases to 90.0% of its final value in 3.00 s. Induction - Spring 2006 36 16. Show that I = I0 e – t/τ is a solution of the differential equation where τ = L/R and I0 is the current at t = 0. Induction - Spring 2006 37 17. Consider the circuit in Figure P32.17, taking ε = 6.00 V, L = 8.00 mH, and R = 4.00 Ω. (a) What is the inductive time constant of the circuit? (b) Calculate the current in the circuit 250 μs after the switch is closed. (c) What is the value of the final steady-state current? (d) How long does it take the current to reach 80.0% of its maximum value? Induction - Spring 2006 38 18. In the circuit shown in Figure P32.17, let L = 7.00 H, R = 9.00 Ω, and ε = 120 V. What is the self-induced emf 0.200 s after the switch is closed? Induction - Spring 2006 39 27. A 140-mH inductor and a 4.90-Ω resistor are connected with a switch to a 6.00-V battery as shown in Figure P32.27. (a) If the switch is thrown to the left (connecting the battery), how much time elapses before the current reaches 220 mA? (b) What is the current in the inductor 10.0 s after the switch is closed? (c) Now the switch is quickly thrown from a to b. How much time elapses before the current falls to 160 mA? Induction - Spring 2006 40 32. At t = 0, an emf of 500 V is applied to a coil that has an inductance of 0.800 H and a resistance of 30.0 Ω. (a) Find the energy stored in the magnetic field when the current reaches half its maximum value. (b) After the emf is connected, how long does it take the current to reach this value? Induction - Spring 2006 41 52. The switch in Figure P32.52 is connected to point a for a long time. After the switch is thrown to point b, what are (a) the frequency of oscillation of the LC circuit, (b) the maximum charge that appears on the capacitor, (c) the maximum current in the inductor, and (d) the total energy the circuit possesses at t = 3.00 s? Induction - Spring 2006 42 Back to Variable Sources Induction - Spring 2006 43 Source Voltage: emf V V0 sin( t ) Induction - Spring 2006 44 Average value of anything: T h T f (t )dt 0 h 1 h T T f (t )dt 0 T Area under the curve = area under in the average box Induction - Spring 2006 45 Average Value T 1 V V (t )dt T0 For AC: T 1 V V0 sin t dt 0 T0 Induction - Spring 2006 46 So … Average value of current will be zero. Power is proportional to i2R and is ONLY dissipated in the resistor, The average value of i2 is NOT zero because it is always POSITIVE Induction - Spring 2006 47 Average Value T 1 V V (t )dt 0 T0 Vrms V Induction - Spring 2006 2 48 RMS Vrms V02 Sin 2t V0 1 2 2 Sin ( t )dt T 0 T T 1 T 2 2 2 Sin ( t )d t T 2 0 T T T Vrms V0 Vrms V0 2 Vrms V0 2 2 V0 0 Sin ( )d 2 2 Induction - Spring 2006 49 Usually Written as: Vrms V peak 2 V peak Vrms 2 Induction - Spring 2006 50 Example: What Is the RMS AVERAGE of the power delivered to the resistor in the circuit: R E ~ Induction - Spring 2006 51 Power V V0 sin( t ) V V0 i sin( t ) R R 2 2 V V 0 2 2 0 P(t ) i R sin( t ) R sin t R R Induction - Spring 2006 52 More Power - Details 2 V02 V P Sin 2t 0 Sin 2t R R P P P P V02 R 2 V0 R V02 R V02 R 1 T 2 T Sin 2 (t )dt 0 T 1 0 Sin 2 (t )dt 2 V 1 2 2 0 1 Sin ( )d 2 0 R 2 2 1 1 V0 V0 Vrms 2 R 2 2 R Induction - Spring 2006 53 AC Circuits April 17, 2006 Induction - Spring 2006 54 Last Days … If you need to, file your taxes TODAY! Due at midnight. Note: File on Web has been updated. This week Monday & Wednesday – AC Circuits followed by problem based review Friday – Review problems Next Week Monday – Complete Problem review. Induction - Spring 2006 55 Final Examination Will contain 8-10 problems. One will probably be a collection of multiple choice questions. Problems will be similar to WebAssign problems. Class problems may also be a source. You have 3 hours for the examination. SCHEDULE: MONDAY, MAY 1 @ 10:00 AM http://pegasus.cc.ucf.edu/%7Eenrsvc/registrar/calend ar/exam/ Induction - Spring 2006 56 Back to AC Induction - Spring 2006 57 Resistive Circuit We apply an AC voltage to the circuit. Ohm’s Law Applies Induction - Spring 2006 58 Consider this circuit e iR emf i R CURRENT AND VOLTAGE IN PHASE Induction - Spring 2006 59 Induction - Spring 2006 60 Alternating Current Circuits An “AC” circuit is one in which the driving voltage and hence the current are sinusoidal in time. V(t) Vp v 2 t V = VP sin (t - v ) I = IP sin (t - I ) -Vp is the angular frequency (angular speed) [radians per second]. Sometimes instead of we use the frequency f [cycles per second] Induction - Spring 2006 Frequency f [cycles per second, or Hertz (Hz)] 2 f 61 Phase Term V = VP sin (wt - v ) V(t) Vp 2 t v -Vp Induction - Spring 2006 62 Alternating Current Circuits V = VP sin (t - v ) I = IP sin (t - I ) I(t) V(t) Ip Vp Irms Vrms v -Vp 2 t I/ t -Ip Vp and Ip are the peak current and voltage. We also use the “root-mean-square” values: Vrms = Vp / 2 and Irms=Ip / 2 v and I are called phase differences (these determine when Induction - Spring 2006 63 V and I are zero). Usually we’re free to set v=0 (but not I). Example: household voltage In the U.S., standard wiring supplies 120 V at 60 Hz. Write this in sinusoidal form, assuming V(t)=0 at t=0. Induction - Spring 2006 64 Example: household voltage In the U.S., standard wiring supplies 120 V at 60 Hz. Write this in sinusoidal form, assuming V(t)=0 at t=0. This 120 V is the RMS amplitude: so Vp=Vrms 2 = 170 V. Induction - Spring 2006 65 Example: household voltage In the U.S., standard wiring supplies 120 V at 60 Hz. Write this in sinusoidal form, assuming V(t)=0 at t=0. This 120 V is the RMS amplitude: so Vp=Vrms 2 = 170 V. This 60 Hz is the frequency f: so =2 f=377 s -1. Induction - Spring 2006 66 Example: household voltage In the U.S., standard wiring supplies 120 V at 60 Hz. Write this in sinusoidal form, assuming V(t)=0 at t=0. This 120 V is the RMS amplitude: so Vp=Vrms 2 = 170 V. This 60 Hz is the frequency f: so =2 f=377 s -1. So V(t) = 170 sin(377t + v). Choose v=0 so that V(t)=0 at t=0: V(t) = 170 sin(377t). Induction - Spring 2006 67 Review: Resistors in AC Circuits R E ~ EMF (and also voltage across resistor): V = VP sin (t) Hence by Ohm’s law, I=V/R: I = (VP /R) sin(t) = IP sin(t) (with IP=VP/R) V I 2 t Induction - Spring 2006 V and I “In-phase” 68 Capacitors in AC Circuits C Start from: q = C V [V=Vpsin(t)] Take derivative: dq/dt = C dV/dt So I = C dV/dt = C VP cos (t) E ~ I = C VP sin (t + /2) V I 2 t This looks like IP=VP/R for a resistor (except for the phase change). So we call Xc = 1/(C) the Capacitive Reactance The reactance is sort of like resistance in that IP=VP/Xc. Also, the current leads the voltage by 90o (phase difference). Induction - Spring 2006 V and I “out of phase” by 90º. I leads V by 90º. 69 I Leads V??? What the **(&@ does that mean?? 2 V 1 I Phase= -(/2) I = C VP sin (t + /2) Induction - Spring 2006 Current reaches it’s maximum at an earlier time than the voltage! 70 Capacitor Example A 100 nF capacitor is connected to an AC supply of peak voltage 170V and frequency 60 Hz. C E ~ What is the peak current? What is the phase of the current? 2f 2 60 3.77 rad/sec C 3.77 107 1 XC 2.65M C I=V/XC - Spring 2006 by 90o (phase difference). 71 Also, the current Induction leads the voltage Inductors in AC Circuits ~ L V = VP sin (t) Loop law: V +VL= 0 where VL = -L dI/dt Hence: dI/dt = (VP/L) sin(t). Integrate: I = - (VP / L cos (t) or V Again this looks like IP=VP/R for a resistor (except for the phase change). I I = [VP /(L)] sin (t - /2) 2 t So we call the XL = L Inductive Reactance Here the current lags the voltage by 90o. Induction by - Spring 2006 I lags V by 90º. V and I “out of phase” 90º. 72 Induction - Spring 2006 73 Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Vp Ip t Induction - Spring 2006 74 Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Capacitor Vp Ip Ip t t Induction - Spring 2006 Vp 75 Phasor Diagrams A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. The “y component” is the actual voltage or current. Resistor Capacitor Inductor Vp Ip t Vp Ip Induction - Spring 2006 Vp Ip 76 Steady State Solution for AC Im Current (2) I m d L cos d I m R sin d t cos d t m sin d t d C • Expand sin & cos expressions sin d t sin d t cos cos d t sin cos d t cos d t cos sin d t sin High school trig! • Collect sindt & cosdt terms separately cosdt terms d L 1/ d C cos R sin 0 sindt terms I m d L 1/ d C sin I m R cos m • These equationsInduction can- Spring be2006solved for Im and 77 (next slide) Steady State Solution for AC Im Current (2) I m d L cos d I m R sin d t cos d t m sin d t d C • Expand sin & cos expressions sin d t sin d t cos cos d t sin cos d t cos d t cos sin d t sin High school trig! • Collect sindt & cosdt terms separately cosdt terms d L 1/ d C cos R sin 0 sindt terms I m d L 1/ d C sin I m R cos m • These equationsInduction can- Spring be2006solved for Im and 78 (next slide) Steady State Solution for AC Current (3) d L 1/ d C cos R sin 0 I m d L 1/ d C sin I m R cos m • Solve for and Im in terms of tan d L 1/ d C R X XC L R Im m Z • R, XL, XC and Z have dimensions of resistance X L d L Inductive “reactance” X C 1/ d C Capacitive “reactance” Z R2 X L X C 2 Total “impedance” • Let’s try to understand this solution using “phasors” Induction - Spring 2006 79 REMEMBER Phasor Diagrams? A phasor is an arrow whose length represents the amplitude of an AC voltage or current. The phasor rotates counterclockwise about the origin with the angular frequency of the AC quantity. Phasor diagrams are useful in solving complex AC circuits. Resistor Capacitor Inductor Vp Ip Vp Ip t Ip t t Induction - Spring 2006 Vp 80 Reactance - Phasor Diagrams Resistor Capacitor Inductor Vp Ip Vp Ip t Ip t t Induction - Spring 2006 Vp 81 “Impedance” of an AC Circuit R L ~ C The impedance, Z, of a circuit relates peak current to peak voltage: Ip Vp Z Induction - Spring 2006 (Units: OHMS) 82 “Impedance” of an AC Circuit R L ~ C The impedance, Z, of a circuit relates peak current to peak voltage: Ip Vp Z (Units: OHMS) (This is the ACInduction equivalent of Ohm’s law.) - Spring 2006 83 Impedance of an RLC Circuit R E ~ L C As in DC circuits, we can use the loop method: E - V R - VC - VL = 0 I is same through all components. Induction - Spring 2006 84 Impedance of an RLC Circuit R E ~ L C As in DC circuits, we can use the loop method: E - V R - VC - VL = 0 I is same through all components. BUT: Voltages have different PHASES they add as PHASORS. Induction - Spring 2006 85 Phasors for a Series RLC Circuit Ip VLp VRp (VCp- VLp) VP VCp Induction - Spring 2006 86 Phasors for a Series RLC Circuit Ip VLp VRp (VCp- VLp) VP VCp By Pythagoras’ theorem: (VP )2 = [ (VRp )2 + (VCp - VLp)2 ] Induction - Spring 2006 87 Phasors for a Series RLC Circuit Ip VLp VRp (VCp- VLp) VP VCp By Pythagoras’ theorem: (VP )2 = [ (VRp )2 + (VCp - VLp)2 ] 2 + (I 2 - Spring 2006- I X ) = Ip2 RInduction X p C p L 88 Impedance of an RLC Circuit R Solve for the current: Ip ~ L C Vp Vp Z R2 (X c X L )2 Induction - Spring 2006 89 Impedance of an RLC Circuit R Solve for the current: Ip ~ L C Vp Z R2 (X c X L )2 Impedance: Vp Z 1 R L C 2 2 Induction - Spring 2006 90 Impedance of an RLC Circuit Vp Ip Z 1 R L C Z 2 2 The current’s magnitude depends on the driving frequency. When Z is a minimum, the current is a maximum. This happens at a resonance frequency: The circuit hits resonance when 1/C-L=0: r=1/ LC When this happens the capacitor and inductor cancel each other and the circuit behaves purely resistively: IP=VP/R. IP R =10 L=1mH C=10F R = 1 0 0 0 1 0 r 2 1 0 3 Induction - Spring5 2006 4 1 0 1 0 The current dies away at both low and high frequencies. 91 Phase in an RLC Circuit Ip VLp We can also find the phase: VRp (VCp- VLp) VP tan = (VCp - VLp)/ VRp or; or VCp tan = (XC-XL)/R. tan = (1/C - L) / R Induction - Spring 2006 92 Phase in an RLC Circuit Ip VLp We can also find the phase: VRp (VCp- VLp) VP tan = (VCp - VLp)/ VRp or; or VCp tan = (XC-XL)/R. tan = (1/C - L) / R More generally, in terms of impedance: cos R/Z At resonance the phase goes to zero (when the circuit becomes purely resistive, the current and- Spring voltage Induction 2006 are in phase). 93 Power in an AC Circuit V = 0 V(t) = VP sin (t) I 2 I(t) = IP sin (t) t (This is for a purely resistive circuit.) P P(t) = IV = IP VP sin 2(t) Note this oscillates twice as fast. 2 t Induction - Spring 2006 94 Power in an AC Circuit The power is P=IV. Since both I and V vary in time, so does the power: P is a function of time. Use, V = VP sin (t) and I = IP sin ( t+ ) : P(t) = IpVpsin(t) sin ( t+ ) This wiggles in time, usually very fast. What we usually care about is the time average of this: 1 T P 0 P( t )dt T Induction - Spring 2006 (T=1/f ) 95 Power in an AC Circuit Now: sin( t ) sin( t )cos cos(t )sin Induction - Spring 2006 96 Power in an AC Circuit Now: sin( t ) sin( t )cos cos(t )sin P( t ) I PVP sin( t )sin( t ) I PVP sin 2( t )cos sin( t )cos( t )sin Induction - Spring 2006 97 Power in an AC Circuit Now: sin( t ) sin( t )cos cos(t )sin P( t ) I PVP sin( t )sin( t ) I PVP sin 2( t )cos sin( t )cos( t )sin Use: and: So sin ( t ) 2 1 2 sin( t ) cos( t ) 0 P 1 2 I PV P cos Induction - Spring 2006 98 Power in an AC Circuit Now: sin( t ) sin( t )cos cos(t )sin P( t ) I PVP sin( t )sin( t ) I PVP sin 2( t )cos sin( t )cos( t )sin Use: and: So sin ( t ) 2 1 2 sin( t ) cos( t ) 0 P 1 2 I PV P cos which we usually writeInduction as - Spring P2006 IrmsVrms cos 99 Power in an AC Circuit P IrmsVrms cos goes from -900 to 900, so the average power is positive) cos( is called the power factor. For a purely resistive circuit the power factor is 1. When R=0, cos()=0 (energy is traded but not dissipated). Usually the power factor depends on frequency. Induction - Spring 2006 100