* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download ENT 163 03-08 - UniMAP Portal
Valve RF amplifier wikipedia , lookup
Josephson voltage standard wikipedia , lookup
Schmitt trigger wikipedia , lookup
Operational amplifier wikipedia , lookup
Power electronics wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Two-port network wikipedia , lookup
Power MOSFET wikipedia , lookup
Surge protector wikipedia , lookup
Current source wikipedia , lookup
Rectiverter wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Opto-isolator wikipedia , lookup
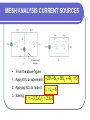
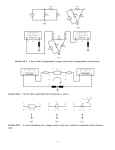
ENT 163 FUNDAMENTALS OF ELECTRICAL ENGINEERING LECTURE #3 METHODS OF ANALYSIS HASIMAH ALI Programme of Mechatronics, School of Mechatronics Engineering, UniMAP. Email: [email protected] Contents • Introduction • Nodal Analysis • Nodal Analysis with Voltage Sources • Mesh Analysis • Mesh Currents with Current Sources INTRODUCTION Two powerful techniques for circuit analysis: 1. Nodal analysis ( application of KCL) 2. Mesh analysis ( application of KVL) NODAL ANALYSIS 1. In nodal analysis, we are interested in finding the node voltages. 2. Steps to determine node voltage: 1. Select reference node. 2. Assign voltage v1, v2, ......vn 1, to the remaining n-1 nodes (with respect to reference node) 3. Apply KCL to each nonreference nodes. Use Ohm’s Law to express the branch currents. 4. Solve the resulting simultaneously equations to solve for node voltage NODAL ANALYSIS The first step is selecting a node as the reference or datum node. The reference node is commonly called the ground since it is assumed to have zero potential. NODAL ANALYSIS Consider the above figure as an example: 1. Ground has been chosen as the reference node 2. Assign v1 and v2 as node 1 and 2 respectively. (node voltage = voltage of node with respect to the reference node). 3. Apply KCL: Node1 : I1 I 2 i1 i2 Node2 : I 2 i2 i3 NODAL ANALYSIS Apply Ohm’s Law, where current flows from a higher potential to a lower potential in a resistor: i We obtain: vhigher vlower R v1 0 v1 v2 v2 0 i1 , i2 , i3 R1 R2 R3 Substitute into equation: I1 I 2 I2 v1 v1 v2 R1 R2 v1 v2 v 2 R2 R3 Solve for v1 and v2 using elimination technique/ Cramer’s rule. NODAL ANALYSIS Example 3.1: Calculate the node voltages in the circuit shown in Figure 1. NODAL ANALYSIS Solution: Using the elimination technique NODAL ANALYSIS Practice Problem Obtain the node voltages in the circuit in Fig shown. Answer: v1= -2V, v2 = -14V NODAL ANALYSIS Example 3.2: Determine the voltages at the nodes in Figure shown. Solution: NODAL ANALYSIS We have three simultaneous equation to solve to get the node voltages v1,v2, v3. Using elimination technique NODAL ANALYSIS WITH VOLTAGE SOURCES Possibilities: 1. If a voltage source is connected between the reference node and a nonrefence node, simply set the voltage at the nonreference node equal to the voltage of the voltage source 2. If the voltage is connected between two nonreference nodes, the two nonreference nodes from a generalized node or supernode; apply both KCL and KVL to determine the node voltages. Supernode: formed by enclosing voltage source connected between two nonreference nodes and any elements connected in parallel with it. NODAL ANALYSIS WITH VOLTAGE SOURCES From the figure: • v1 = 10V • Nodes 2 and 3 form a supernode • KCL at supernode: i1 i4 i2 i3 v1 v2 v4 v3 v2 0 v3 0 2 4 8 6 KVL at supernode: v2 5 v3 0 v2 v3 5 NODAL ANALYSIS WITH VOLTAGE SOURCES Practice Problem: Find v and i in the circuit in Fig 3.11: Answer: -0.2V, 1.4A NODAL ANALYSIS WITH VOLTAGE SOURCES Practice problem: For the circuit shown in Figure 3.9, find the node voltages. Answer: v1= -7.333V, v2= -5.333V MESH ANALYSIS 1. Mesh analysis is also known as loop analysis or the mesh-current method. 2. Mesh is a loop which does not contain any other loops within it. 3. Application: to find unknown currents 4. Only capable to a planar circuit 5. Planar circuit: can be drawn in a plane with no branches crossing one another. 6. A circuit may have crossing branches and still be planar if it can be redrawn such that it has no crossing branches. MESH ANALYSIS Fig. 3.15 a) a Planar circuit with crossing branches. b)The same circuit redrawn with no crossing branches b) MESH ANALYSIS Steps in determining node voltage: 1. Assign mesh currents i1,i2,…in to the n meshes 2. Apply KVL to each of the n meshes. Use Ohm’s Law to express the voltages in terms of the mesh currents. 3. Solve the resulting n simultaneously equations to get the mesh currents. MESH ANALYSIS Consider the figure below: 1. Assign i1 and i2 as meshes 1 and 2. 2. Apply KVL to each mesh: Mesh1 : V1 R1i1 R3 (i1 i2 ) 0 Mesh 2 : R2i2 V2 R3 (i2 i1 ) 0 3. Solve for mesh currents i1 and i2 MESH ANALYSIS Example: For the circuit in Figure, find the branch currents I1, I2 and I3 using mesh analysis. MESH ANALYSIS Practice Problem: Calculate the mesh currents i1 and i2 in the circuit of Figure shown. Answer: i1= 2/3 A, i2=0A MESH ANALYSIS CURRENT SOURCES Possibilities: 1. When a current source exists only in one mesh – set the current as equal to the source. • set i2 = -5A • Mesh equation: 10 4i1 6(i1 i2 ) 0, i1 2 A MESH ANALYSIS CURRENT SOURCES 1. When the current source exists between two meshes – create a supermesh (by excluding the current source and any elements connected in series with it). A supermesh results when two meshes have a (dependent or independent) current source in common. Fig: a) Two meshes having a current source in common, b) a supermesh, created by excluding the current source MESH ANALYSIS CURRENT SOURCES • From the above figure: 1. Apply KVL to supermesh: 20 6i1 10i2 4i2 0 2. Applying KCL to node 0: i2 i1 6 3. Solving: i1 3.2 A, i2 2.8 A MESH ANALYSIS CURRENT SOURCES Problem: For the circuit shown, find i1 to i4 using mesh analysis. MESH ANALYSIS CURRENT SOURCES Solution: Applying KVL to the larger supermesh, MESH ANALYSIS CURRENT SOURCES Properties of a supermesh: 1. The current source in the supermesh provides the constraint. 2. A supermesh has no current of its own. 3. A supermesh requires the application of both KVL and KCL FURTHER READING 1. Fundamentals of Electric Circuits, 2nd Edition,McGrawhill Alexander, C. K. and Sadiku, M. N. O. 2. Electric Circuit, 8th Edition, Pearson, Nillson and Riedel