* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PowerPoint: Self induction in a coil and Back
Josephson voltage standard wikipedia , lookup
Index of electronics articles wikipedia , lookup
Audio power wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Magnetic core wikipedia , lookup
Radio transmitter design wikipedia , lookup
Schmitt trigger wikipedia , lookup
Crystal radio wikipedia , lookup
Operational amplifier wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current source wikipedia , lookup
Power MOSFET wikipedia , lookup
Surge protector wikipedia , lookup
Voltage regulator wikipedia , lookup
Opto-isolator wikipedia , lookup
Current mirror wikipedia , lookup
Power electronics wikipedia , lookup
Switched-mode power supply wikipedia , lookup
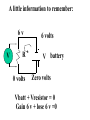
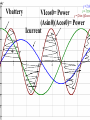
130 volts / 1.4 ohms = 93 amperes! What if this coil were connected to 130 v ac??? VI = 12,000 watts ! It would melt down!!!! The Resistance is 1.4 ohms Ohm meter P T P T The actual current is 3.45 amperes AC. Input voltage is 130 V. 450 watts ???????? Why is the current so small? And why doesn’t the coil even get warm? 130 v In fact, there are almost zero watts A little information to remember: 6v V R 0 volts 6 volts V battery Zero volts Vbatt + Vresistor = 0 Gain 6 v + lose 6 v =0 V Voltmeter AC R Resistor Power Source Vapplied+Vinduced=0 Power Voltage Current Current and Voltage in in PHASE; therefore, the Power curve is in phase with them both. Current in coil and resistor Induced voltage in coil O Prop I Flux in the coil follows VL = - this curve also to we expect t maximum induced voltage to be where the flux is changing at the highest rate. Signal generator voltage Va Current in coil Induced voltage VL The voltages around a loop must add up to zero so the sum of Vsignal gen + VL = O A coil in series with an AC power source: V coil AC POWER SOURCE Vapplied Voltmeter Vapplied + Vinduced=0 Vapplied current Vinduced http://ostc.physics.uiowa.edu/~wkchan/E LECTENG/AC_POWER/AC.html Power = V battery x I battery Output voltage of signal generator Current out of signal generator Power output taken from the signal generator would be: P=VI If these are multiplied the puzzle is solved. Signal generator voltage Va Current in coil Induced voltage VL The voltages around a loop must add up to zero so the sum of Vsignal gen + VL = O (Vmax Cos 0 ) (I max Sin 0) = Power - + + Flux building up Energy being stored and given back. Why is there no heat being generated in the coil? …what energy is taken from the battery is given back so there is NO heating of the coil. Power = (Va )( I) cos O = zero! Theta is the angle between the two curves…in this case 90 degrees. Cos 90 degrees = zero Now, why is the current so much lower than expected? If we use I=V/R it must be because somehow the resistance of the coil is larger to AC than to DC. The resistance of a coil to AC current is given by the F L where F is the frequency equation: Rcoil = 2 and L the inductance of coil. L for the coil is 0.10 henrys. F = 60 hz R then = 38 ohms. I= V/R = 130 v/38 ohms = 3.4 amps. The resistance of the coil if proportional to both the frequency and L. As f increases the resistance gets larger…. Choking off the current. Vbattery VIcos0= Power (Asin0)(Acos0)= Power Icurrent + _ Power = VI (+) I (+) (-) V The power taken from the signal generator (+) balances the power given back (-) and therefore no heat is produced in the coil even though the current is 3.4 amps! Power Vapplied Current Time (s) Vinduced Vapplied An arrangement for viewing the phase relationship between current in and voltage across a coil. A signal generator is connected in series with a coil and a resistor. An oscilloscope (for viewing how voltage changes in time) is connected (via computer) to both the coil and resistor. VL Signal Gen gnd VR R coil VL VR Gnd Current is min voltage is max. Current is max voltage is min. The current in coil and resistor are the same. The voltage across the resistor is in phase with the current so we can see the phase relationship between current and voltage of the coil. ac Power Capacitor Power Vapplied Current Time (s) Vinduced Vapplied Inductor