* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 4_internal_resistanc..
Power electronics wikipedia , lookup
Electric battery wikipedia , lookup
Surge protector wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Negative resistance wikipedia , lookup
Power MOSFET wikipedia , lookup
Rechargeable battery wikipedia , lookup
Switched-mode power supply wikipedia , lookup
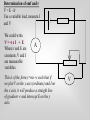
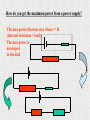
Electromotive Force and Internal Resistance Current Potential Difference Before we start, the golden rules from GCSE: The ? through any components connected in series is the same through each component. The ? across any components connected in parallel is the same across each component. The PD between the terminals of a cell is caused by a chemical reaction within the cell. The voltage produced is known as the Electromotive force (EMF.) As soon as we draw current from the cell or battery, a p.d. is produced over any internal resistance in the cell. (The cell is made of metals which have resistance!) This p.d. reduces the voltage we can measure across the terminals of the cell - the terminal p.d. emf Internal Resistance An ideal cell is easy to deal with so we invent a model of a real cell as being made up of a fixed resistor (representing the internal resistance (r)) and a cell with no internal resistance of emf E. E emf r Internal Resistance Typical value E for a cell is 1.5V. Terminal p.d. will be a little less. The Terminal p.d. (V) will be equal to the p.d. across the load. E r V Try to explain the following equations: V=IR p.d. lost across internal resistance = Ir Terminal p.d. = E - Ir V = E - Ir E = V +Ir E = IR + Ir E = I(R+r) You can learn these if you want to but it is much better to understand and be able to construct them yourself. Questions: 1 A battery has an internal resistance of 2 and an emf of 6V. What is the current drawn and terminal p.d. when a load of 8 is applied to it? Solution: Draw a diagram: 6V 2 I/A 8 6V Questions: 1 A battery has an internal resistance of 2 and an emf of 6V. What is the current drawn and terminal p.d. when a load of 8 is applied to it? Total Resistance = 2+8 = 10 I=V/R I = 6/10 = 0.6 A V = E - Ir V = 6 - (0.6 x 2) V = 4.8V 2 I /A 8 2 A battery has a terminal p.d. of 1.5V in open circuit and 1.4V with a load of 10. What is the internal resistance of the cell? In open circuit R is infinite, so I is zero. That will make E = V - Ir become V=E so the emf is 1.5V In the second case with a load of 10 using E = V +Ir will give 1.5 = 1.4 +Ir (1) 1.5V But I = V/R so I = 1.4 / 10 = 0.14A ? substituting back into (1) we get 1.5 = 1.4 + (0.14 x r) 1.5 - 1.4 = 0.14 x r r = 0.1 / 0.14 r = 0.714 I /A 10 Determination of emf and r V = E - Ir Use a variable load, measure I and V We could write V = -r x I + E Where r and E are constants, V and I are measurable variables. A This is of the form y=mx+c such that if we plot V on the y axis (ordinate) and I on the x axis, it will produce a straight line of gradient -r and intercept E on the y axis. V Method Determination of emf and r Vary R to obtain sets of values of V and I Plot V against I Determine the y intercept - that will be equal to E Determine the gradient - that will be equal to -r A It is better to plot the graph rather than just substitute the values because: it has the effect of averaging out any errors which are random obvious mistakes are easily seen andV not included. High internal resistance ? the load could have less resistance than r so more power would be developed in the power supply than the load not very good for delivering power but what if the supply was a very high voltage? it would effectively limit the current and terminal p.d. So it is good for a high voltage, low current supply. Low Internal resistance ? very little voltage is lost across the internal resistance most of the power is delivered to the load So it would be good for a car battery providing low voltage and high current to turn the starter motor. How do you get the maximum power from a power supply? The max power theorem says when r = R (internal resistance = load) The max power is developed in the load note: 50% of the energy is wasted producing heat in the supply you get a lot of power but waste a lot of the energy stored in the power supply Resistors in series You could be asked to prove that R = R1 + R2 in an exam! R1 R2 The total pd (V) across the pair of resistors is the sum of the p.d.’s across each one i.e. This would be V = V1 + V2 But V=IR so IR = I1R1 + I2R2 Since they are in series, I = I1 = I2 so R = R1 + R2 typical of a four mark question. That is 4/60 well worth understanding and learning. I1 Resistors in Parallel R1 I I2 R2 We want to find the resistance R that can replace these and draw the same current I and have the same pd across it, V. Conservation of charge will show that I = I1 + I2 But I = V/R so V/R = V1/R1 + V2/R2 Since the resistors are in parallel, V = V1 = V2 so 1 1 1 R R1 R2 Don’t be over confident. Many A level students can’t do the maths accurately. To add fractions you must find a common denominator To solve for R you must eventually turn the equation upside down Question What is the combined resistance of a 5 and 4 resistance connected first in series, then in parallel? In parallel 1 1 1 In series R R = R1 + R2 5+4 = 9 1 R 1 5 1 4 R = 20/9 = 2.2 R1 4 5 5 x 4 R2 9 20