Download Chapter 11: Capacitive Transients, Pulse and

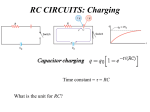
Chapter 11
Capacitive Charging,
Discharging, and
Waveshaping Circuits
Introduction
• Circuit for studying capacitor charging and
discharging.
• Transient voltages and currents result when
the circuit is switched.
Capacitor Charging
• For an uncharged capacitor, at the instant the
switch is closed, the current jumps to E/R,
then decays to zero.
• At the instant of switching, the circuit looks
like a short circuit.
• The voltage across the capacitor begins at
zero and gradually climbs to E volts.
• The capacitor voltage cannot change
instantaneously.
Capacitor Charging
• Because the voltage cannot change
instantaneously, the graphs have the shapes
shown:
Steady State Conditions
• When the voltage and current reach their final
values and stop changing, the circuit is at
steady state.
• The capacitor has voltage across it, but no
current flows through the circuit.
• The capacitor looks like an open circuit to
steady state dc.
Capacitor Discharging
• Assume the capacitor has E volts across
when it begins to discharge.
• The current will jump to -E/R.
• Both voltage and current will decay to zero.
Capacitor Discharging
• Here are the decay waveforms:
Capacitor Charging Equations
• The voltages and currents in a charging
circuit do not change instantaneously.
• These changes over time are exponential
changes.
• The equation for voltage across the capacitor
over time is

vC  E 1  e
 t / RC

Capacitor Charging Equations
• The voltage across the resistor is found from
KVL: E - vC.
v R  Ee t / RC
• The current in the circuit is
E t / RC
iC  e
R
Capacitor Charging Equations
• Values at any time may be
determined from these
equations.
• The waveforms are
shown:
The Time Constant
• The rate at which a capacitor charges
depends on the product of R and C.
• This product is known as the time constant.
•  = RC
•  has units of seconds.
Duration of a Transient
• The length of time that a transient lasts
depends on the exponential function e-t/.
• As t increases, the function decreases, and
when the t reaches infinity, the function
decays to zero.
• For all practical purposes, transients can be
considered to last for only five time constants.
Capacitor with an Initial Voltage
• If the capacitor already has a voltage on it,
this voltage is denoted as V0.
• The voltage and current in a circuit will be
affected by the initial voltage
v C  E  V0  E e
E  V0 t / 
iC 
e
R
t / 
Capacitor Discharging Equations
• If a capacitor is charged to voltage V0 and
then discharged, the equations become
v C  V0 e
t / R
v R  V0 e
t / R
V0  t / R
iC  
e
R
Capacitor Discharge Equations
• Note that the current is negative because it
flows opposite to the reference direction.
• As for the charging phase, discharge
transients last five time constants.
• All voltages and currents are at zero when
the capacitor has fully discharged.
Capacitor Discharge Equations
• The curves shown
represent voltage
and current during
discharge:
More Complex Circuits
• For complex circuits (those with multiple
resistors), you may have to use Thévenin’s
theorem.
• Remove the capacitor and determine the
Thévenin equivalent of the circuit.
• Use RTh to determine .
• Use ETh as the equivalent source voltage.
An RC Timing Application
• RC circuits are used to
create delays for alarm,
motor control, and timing
applications.
• The alarm unit shown
contains a threshold
detector, and when the
input to this detector
exceeds a preset value,
the alarm is turned on.
Simple Waveshaping Circuits
• Circuit (a) provides
approximate
integration if 5>>T.
• Circuit (b) provides
approximate
differentiation if
5>>T.