* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 30: Inductance
Resistive opto-isolator wikipedia , lookup
Stray voltage wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Electric machine wikipedia , lookup
Ignition system wikipedia , lookup
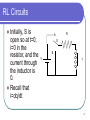
Electrical ballast wikipedia , lookup
Surge protector wikipedia , lookup
Skin effect wikipedia , lookup
Opto-isolator wikipedia , lookup
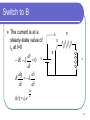
Current source wikipedia , lookup
Magnetic core wikipedia , lookup
Rectiverter wikipedia , lookup
Alternating current wikipedia , lookup
Chapter 30 1 Mutual Inductance Consider a changing current in coil 1 We know that B1=m0i1N1 And if i1 is changing with time, dB1/dt=m0N1 d(i1)/dt But a changing B-field across coil 2 will initiate an EMF2 such that EMF2=-N2A2 dB1/dt Since dB1/dt is proportional to di1/dt then the EMF2 Where M is the mutual inductance which is based on the sizes of the coils, and the number of turns di1 dt di1 EMF2 M dt 2 Mutual-mutual Inductance But it could be that the changes are happening in coil 2. Then EMF1 di2 dt di2 EMF1 M dt It turns out that this value of M is identical to the previously discussed M so EMF1 M di2 dt and EMF2 M di1 dt where M N 2 B 2 N1 B1 i1 i2 3 My favorite unit—the henry The Henry (H) is the unit of inductance Equivalent to: 1H=1 Wb/A = 1 V*s/A = 1 W*s = 1 J/A2 H is large unit; typically we use small units such as mH and mH. 4 Self Inductance But a coil of wire with a changing current can produce an EMF within itself. This EMF will oppose whatever is causing the changing current So a coil of wire takes on a special name called the inductor 5 Inductor Definition of inductance is the magnetic flux per current (L) For an N-turn solenoid, L is L= N/I N turns= (n turns/length)*(l length) The near center solution of inductance depends only on geometry Electrical symbol N nlBA where B m 0in N m 0 n 2liA N If L i L m 0 n 2lA Near center L m0 n 2 A l 6 Inductor N If L Li N i and if d di EMF N L dt dt Electrical symbol Again, the EMF acts to oppose the change in current i (increasing) i (decreasing) High potential VL acts like a Low potential Low potential VL acts like a High potential 7 RL Circuits Initially, S is open so at t=0, i=0 in the resistor, and the current through the inductor is 0. Recall that i=dq/dt R A S B V L 8 Switch to A Initially, the inductor acts against the changing current but after a long time, it behaves like a wire Rt V L i 1 e and R S H i V di iR L V 0 dt di V iR L dt Ansatz R A B L L di V RtL e dt L 9 Voltage across the resistor and inductor Potential across resistor, VR VR iR Rt Rt V 1 e L R V 1 e L R R A S Potential across capacitor, VC B V L di V RtL VL L L e dt L VL Ve Rt L At t=0, VL=V and VR=0 At t=∞, VL=0 and VR=V 10 L/R—Another time constant L/R is called the “time constant” of the circuit L/R has units of time (seconds) and represents the time it takes for the current in the circuit to reach 63% of its maximum value When L/R=t, then the exponent is -1 or e-1 tL=L/R 11 Switch to B The current is at a steady-state value of i0 at t=0 di iR L 0 dt dq di R L dt dt i (t ) i0 e V R A S B L Rt L 12 Energy Considerations di Rate at which energy is supplied from battery V L dt and P Vi Rate at which energy is stored in the magnetic field of the inductor di Vi Li dt Energy of the magnetic field, UB dU B di P Li dt dt 1 2 1 2 U B Li (recall KE mv ) 2 2 13 Energy Density, u Consider a solenoid of area A and length, l UB U B volume A l 1 2 Li L 2 u but m0 n 2 A Al l 1 u m 0 n 2i 2 but B m 0in 2 0E2 B2 uB and uE 2m0 2 u Energy stored at any point in a magnetic field Energy stored at any point in a magnetic field 14 L-C Oscillator – The Heart of Everything di q 0 dt C dq di d dq d 2 q i 2 dt dt dt dt dt d 2q q d 2q 1 L 2 0 2 q0 dt C dt LC Ansatz : q Q cost dq Q sin t i dt d 2q 2Q cost 2 dt so 1 2Q cost Q cost 0 LC 1 1 2 0 2 LC LC L L C If the capacitor has a total charge, Q 15 Perpetual Motion? 16 Starting Points Charge q Current i t The phase angle, , will determine when the maximum occurs w.r.t t=0 The curves above show what happens if the current is 0 at t=0 17 Energy considerations A quick and dirty way to solve for i at any time t in terms of Q & q At t=0, the total energy in the circuit is the energy stored in the capacitor, Q2/2C At time t, the energy is shared between the capacitor and inductor (q2/2C)+(1/2 Li2) Q2/2C= (q2/2C)+(1/2 Li2) i 1 Q2 q2 LC 18 Oscillators is oscillators is oscillators 19 Give me an “R”! Consider adding a resistor, R to the circuit The resistor dissipates the energy. For example, consider a child on a swing. His/her father pushes the child and gets the child swinging. In a perfect system, the child will continue swinging forever. The resistor provides the same action as if the child let their feet drag on the ground. The amplitude of the child’s swing becomes smaller and smaller until the child stops. The current in the LRC circuit oscillates with smaller and smaller amplitudes until there is no more current 20 Mathematically di q iR 0 dt C dq di d 2 q i 2 dt dt dt d 2q dq q L 2 R 0 dt dt C Ansatz L q (t ) Qe where Rt 2L If R is small, underdamped When oscillation stops due to R, critically damped Very large values of R, overdamped cos t R2 2 4L 2 21 Why didn’t I use a voltage source? The practical applications of the LC, LR, and LRC circuits depend on using a sinusoidally varying voltage source: An AC voltage source 22