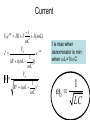Download Lab #1: Ohm’s Law (and not Ohm’s Law)

Lab #6: the LRC Circuit and
Resonance: part I
• remember how AC circuits containing a cap,
an inductor, and a resistor in series behave
• experience resonance experimentally
• two week lab. Only 1 lab report. (so, no lab
report due next week. A bigish lab report due
the following week)
• this week: pgs 56- 57. next week pg 61
LRC Circuit
Phenomena of
resonance an important
one in physics
Impedance:
Resistor:
Capacitor:
Inductor:
R
i
C
i L
(voltage in phase with current)
(voltage lags current by 90o)
(voltage leads current by 90o)
Current
i
V0e  IR  I
 I (i L)
C
V0
I
e it
1
( R  i ( L 
))
C
V0
I 
1 2
2
R  ( L 
)
C
it
I is max when
denominator is min:
when  L=1/ C
0 
1
LC
Resonance
Resonance
  L/R
  1 /  (width of resonance, VR =Vmax / 2)
0
L
Q


R 2C
phases
i
V0e  IR  I
 I (i L)
C
V0
I
e  it  I e  i (t  )
1
( R  i ( L 
))
C
V0
I 
1 2
R 2  ( L 
)
C
1
Phase of current (and thus
L 
voltage across R) with
C
tan  
respect to V0
R
it
Phase shift between voltage across resistor and
input is zero when at resonant frequency
phases
Note that since
VL leads by 90
degrees and Vc
lags by 90
degrees, they
are always outof-phase by 180
degrees
IMPORTANT!!!!!
• Replace C-1 with
Vary the input frequency using the following values:
(f=f0x(0.1,0.5,0.6,0.75,0.9,1.0,1.1,1.25,1.4,1.5,1.9,2.3)
For each value, record the amplitudes of V0 and VR as well
as the frequency f and the phase shift phi (from the time shift
of the peaks) between V0 and VR. Calculate XL= L and
XC=1/ C using the measured values for L and C.
• Also, in C-3, only do the first sentence.
Hints
• part A1.
200 mH: make this by putting 2 100 mH inductors in
series. Because the mutual inductance is non-negligible, please be
sure to wire them together, measure the inductance, and then put
them into the circuit wired exactly as when you measured them.
• Part A1. assume the uncertainty on internal resistance of the
waveform generator is 2 ohms. (50+-2)
• C-1 at low frequency, wave form can be ugly. Measure to the
average over the “features”. So, need to use cursors, not “measure”
• C-1 don’t assume V0 does not change, monitor it and check that it
does not change
• C-1 note phase shift changes sign.
Lab Exam
• Dec 1,2
• The question bank is attached to the web
page for this class
Some Derivatives
Q
L
1 L

R 2C R C
Q 1  L 
  2 
L 2  R C 
1/2
Q 1  L 
  2 
C 2  R C 
1/2
1
1 1
 Q
2
RC 2 L
L
1 1

Q
2 2
RC
2 C
Q 1 L
1
 2
 Q
R R C
R
d tan 2 
1

d
cos 2 
Schedule
• next week is makeup (Nov 3,4). I have William scheduled for Lab 3 on
Nov 3 and Justin for Lab 2 on Tuesday. Let me know if you need to make
up a lab and are not on this list.
• Lab 6 Lab report is thus due on our next class, Nov 10, 11
Step-wave input
Charge on cap rings at resonant frequency while
decaying away
Like striking a bell
with a hammer
Tosc 
L
 2
R

2
osc
 
2
0
1
2
2
 osc
At large R
Critically damped: R is large
4 L no1oscillation
2
enoughRso
that

2
C  1
occurs
Hints
• Capture a wave form of the ringing with
wavestar
• for part C, only vary R and only give a
qualitative answer