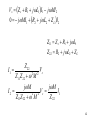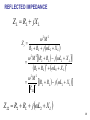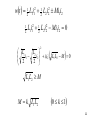* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download EEE 302 Lecture 11 - Universitas Udayana
Immunity-aware programming wikipedia , lookup
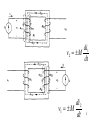
Resistive opto-isolator wikipedia , lookup
Radio transmitter design wikipedia , lookup
Surge protector wikipedia , lookup
Power electronics wikipedia , lookup
Power MOSFET wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Operational amplifier wikipedia , lookup
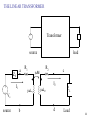
Opto-isolator wikipedia , lookup
Magnetic core wikipedia , lookup
Index of electronics articles wikipedia , lookup
Power dividers and directional couplers wikipedia , lookup
Current source wikipedia , lookup
Distributed element filter wikipedia , lookup
Crystal radio wikipedia , lookup
Valve audio amplifier technical specification wikipedia , lookup
Loading coil wikipedia , lookup
Switched-mode power supply wikipedia , lookup
RLC circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Two-port network wikipedia , lookup
Antenna tuner wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Rectiverter wikipedia , lookup
Standing wave ratio wikipedia , lookup
Magnetically Coupled Networks 1 Magnetically Coupled Networks • A new four-terminal element, the transformer, is introduced in this chapter • A transformer is composed of two closely spaced inductors, that is, two or more magnetically coupled coils – primary side is connected to the source – secondary side is connected to the load 2 di1 v2 M dt di 2 v1 M dt 3 Dot Convention • dot convention: dots are placed beside each coil (inductor) so that if the currents are entering (or leaving) both dotted terminals, then the fluxes add • right hand rule says that curling the fingers (of the right hand) around the coil in the direction of the current gives the direction of the magnetic flux based on the direction of the thumb • We need dots on the schematic to know how the coils are physically oriented out one another 4 Mutually Coupled Coils The following equations define the coupling between the two inductors assuming that each respective current enters the dot side which is also the positive voltage side where L1 and L2 are the self-inductances of the coils (inductors), and M is the mutual inductance between the two coils M i1(t) + v1(t) – L1 i2(t) L2 + v2(t) – d i1 d i2 v1 (t ) L1 M dt dt di di v2 (t ) M 1 L2 2 dt dt 6 EXAMPLE Write a set of mesh-current equations that describe the circuit shown in terms of the currents i1, i2, and i3 7 (In the following set of mesh-current equations, voltage drops appear as positive quantities on the right-hand side of each equation.) Summing the voltages around the first mesh yields d di2 vg 8i1 i2 9 i1 i3 4.5 dt dt The second mesh equation is di2 d 04 4.5 i1 i3 6i2 i3 8i2 i1 dt dt The third mesh equation is d di2 0 9 i3 i1 4.5 6i3 i2 20i3 dt dt 8 Mutually Coupled Coils (AC) • The frequency domain model of the coupled circuit is essentially identical to that of the time domain V1 j L1 I1 j M I 2 V2 j M I1 j L2 I 2 9 Source Input Impedance Linear Transformer The source sees an input impedance, Zi, that is the sum of the primary impedance, and a reflected impedance, ZR, due to the secondary (load) side VS Zi Z P Z R Z P f Z L IP M Z VS + – L1 L2 ZL 10 THE LINEAR TRANSFORMER Transformer source ZS a R2 jωM c I2 I1 jωL1 Vs source R1 load b jωL2 d ZL Load 11 Vs Z s R1 jL1 I1 jMI 2 0 jMI1 R2 jL2 Z L I 2 Z11 Z s R1 jL1 Z 22 R2 jL2 Z L Z 22 I1 V 2 2 s Z11Z 22 M j M j M I2 V I1 2 2 s Z11Z 22 M Z 22 12 Vs Z11Z 22 2 M 2 2M 2 Z int Z11 I1 Z 22 Z 22 Z ab Z11 M 2 Z 22 2 Zs 2M 2 R1 jL1 R2 jL2 Z L 13 REFLECTED IMPEDANCE Z L RL jX L 2M 2 Zr R2 RL j L2 X L 2 M 2 R2 RL j L2 X L R2 RL 2 L2 X L 2 2M 2 Z 22 2 R2 RL j L2 X L Z22 R2 RL jL2 X L 14 EXAMPLE The parameters of a certain linear transformer are R1 = 200 Ω, R2 = 100 Ω, L1 = 9 H, L2 = 4 H, and k = 0.5. The transformer couples an impedance consisting of an 800 Ω resistor in series with a 1 µF capacitor to a sinusoidal voltage source. The 300 V (rms) source has an internal impedance of 500 + j100 Ω and a frequency of 400 rad/s. a) Construct a frequency-domain equivalent circuit of the system. b) Calculate the self-impedance of the primary circuit. c) Calculate the self-impedance of the secondary circuit. d) Calculate the impedance reflected into the primary winding. e) Calculate the scaling factor for the reflected impedance. f) Calculate the impedance seen looking into the primary terminals of the transformer. g) Calculate the rms value of the primary and secondary current. h) Calculate the rms value of the voltage at the terminals of the load and source. i) Calculate the average power delivered to the 800 Ω resistor. j) What percentage of the average power delivered to the transformer is delivered to the load? 15 S0LUTI0N a) frequency-domain equivalent circuit of the system jL1 j 4009 j 3600 ; jL2 j 4004 j1600 ; M 0.5 94 3H ; jM j 4003 j1200 ; 1 106 j 2500 . jC j 400 16 Z11 500 j100 200 j3600 700 j3700 c). The self-impedance of the secondary circuit. Z22 100 j600 800 j 2500 900 j900 d). The impedance reflected into the primary winding. 2 1200 8 900 j900 900 j900 800 j800 Zr 9 900 j900 e). The scaling factor by which Z22* is reflected is 8/9 17 f). The impedance seen looking into the primary terminals of the transformer is the impedance of primary winding plus the reflected impedance, thus Z ab 200 j3600 800 j800 1000 j 4400 g). Calculate I1 and I2 Vs 30000 I1 Z s Z ab 1500 j 4500 20 j 60 63.25 71.57 0 mA rms j 1200 0 I2 I1 59.6363.43 mA rms 900 j900 18 h). The voltages at the terminals of transformer are V2 800 j 2500I 2 156.52 8.820 V rms V1 Z ab I1 1000 j 4400I1 285.385.630 V rms i ). The average power delivered to the load is P 800 I 2 2.84 W 2 19 j). The average power delivered to the transformer is Pab 1000 I1 4.00 W 2 Therefore 2.84 x100 71.11% 4.00 20 Energy Analysis • An energy analysis of the mutually coupled inductors provides an expression for the instantaneous stored energy w(t ) L1i1 (t ) L2 i2 (t ) M i1 (t ) i2 (t ) 1 2 2 1 2 2 • The sign is positive (+) if currents are both entering (or leaving) the dots; sign is negative (-) if currents are otherwise 21 wt L i L i Mi1i2 1 2 1 2 2 11 1 2 2 2 2 L i L i Mi1i2 0 2 11 2 2 2 1 2 2 L1 L2 i1i2 i i 1 2 2 2 L1L2 M 0 L1L2 M M k L1L2 0 k 1 22 Quantifying the Coupling • The mutual inductance, M, is in the range 0 M L1 L2 • The coefficient of coupling (k) between two inductors is defined as 0 k 1 L1 L2 M – for k > 0.5, inductors are said to be tightly coupled – for k 0.5, coils are considered to be loosely coupled 23 DRILL EXERCISE The self-inductances of the coils shown are L1 = 5 mH and L2 = 33.8 mH. If the coefficient of coupling is 0.96, calculate the energy stored in the system in millijoules when (a) i1 = 10 A, i2 = 5 A; (b) i1 = -10 A, i2 = -5 A; (c) i1 = -10 A, i2 = 5 A; and (d) i1 = 10 A, i2 = -5 A. 24