Download Unit 7 - My Teacher Pages

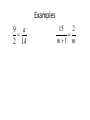
Unit 7
Similarity
Part 1
Ratio / Proportion
• A ratio is a comparison of two quantities by
division.
– You can write a ratio of two numbers a and b,
where b≠0 three ways
• a:b , a to b or
a
b

• When expressing
a ratio in simplest form they
must be the same units of measure

Example
• A bonsai tree is 18 in. wide and stands 2 ft tall.
What is the ratio of the width of the tree to
the height of the tree?
width 18in
18in
18in 3




height 2 ft 2 *12in 24in 4
Example 2
• The measure of two supplementary angles are in
the ratio 1:4. What are the measures of the two
angles?
– Since ratio’s are just reduced fractions we need to find
the value by which they were reduced, x.
1x  4 x  180
5x  180
x  36
So our two angles are 36 and 144,
notice 36:144 reduces to 1:4

Extended Ratio
• An extended ration compares three or more
numbers
• Example: The length of the side a triangle in
the extended ratio 3:5:6. The perimeter of the
triangle is 98 in. Find the length of the longest
side.
3x  5x  6x  98
14 x  98
• The longest side is 42 inch.

x7
Example 2
• The ratio of the sides of a triangle is 7: 9: 12.
The perimeter of the triangle is 84 inch. Find
the length of each side.
– x = 3, 21, 27, 36
• The ratio of the angles of a triangle is 5: 7: 8,
find the measure of each angle.
– x = 9, 45, 63, 72
• Proportion – an equation that states two
ratios are equal
• The first and last numbers if the proportion
are the extremes and the two middle numbers
are the means.
a x

b y
• Cross Product – When solving a proportion
you multiply the extremes and set them equal
to the means

– Example: ay = xb
Examples
15
2

m 1 m
9 a

2 14



Properties of Proportions
a c

b d
a c

b d
a c

b d
Is equivalent to
Is equivalent to

Is equivalent to

b d

a c
a b

c d
ab c d

b
d
Part 2
Similar Polygons
Similar Polygons (6.2)
• Similar Polygons are polygons that have the
same shape but may be different in size.
• Two polygons are similar if and only if their
corresponding angles are congruent and the
measures of their corresponding sides are
proportional!
Scale Factor
• When comparing the length of
corresponding sides you will get a
numerical ratio. This is called the scale
factor.
– They are often given for models of real life
objects. (Tell you how much larger or smaller
and object is)
Example
D
A
10
H
E
8
5
4
2.5
F
B
6
5
C
ABCD ~ EFGH
Because:
A  E , D  H
C  G , B  H
&
AB BC CD DA
=
=
=
EF FG GH HE
3
G