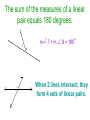Download Warm-up

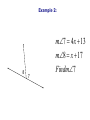
Warm-up
Based on the picture below, tell whether
each statement is true or false.
1. B, C and D are collinear.
2. BCA is a right angle
3. BCD is a straight angle.
4. BC + CD = BD.
Pairs of Angles
Angle and Angle Measures Day
2
Quilt patterns have many sets of angle
pairs.
What do you think the angles
measures have to be so that the
pieces will fit together?
Def: Adjacent Angles
Two angles that are in the same plane and have a common
vertex and a common side but share no interior points.

1 and  2 are adjacent
1 2
They are two separate angles with the same
vertex!!
NOT Adjacent
Def: Linear pair
A linear pair is two adjacent angles (angles with
same vertex) whose non common sides form a line.
3
4
 3 and  4 form a linear pair
The sum of the measures of a linear
pair equals 180 degrees.
7
5 6
7
8
m 7 + m
 8 = 180
8
When 2 lines intersect, they
form 4 sets of linear pairs.
Example 1:
mWYZ = (2x – 5)° and mXYW = (3x + 10)°. Find
the value of x.
Example 2:
m7  4 x  13
m8  x  17
8
Findm7
7
Name two complementary angles:
Name two supplementary angles:
Example 3:
m3  68
Find the complement of angle 3
mB  122
Find the supplement of angle B
Example 4:
ABD and BDC are complementary.
Find the measures of both angles.
ABD  5x  1 and BDC  3x  7
Example 5:
m1  x
Express the complement of 1 in terms of x.
m2 = y
Express the supplement of 2 in terms of y.
Vertical angles are two nonadjacent angles
formed by two intersecting lines. 1 and 3 are
vertical angles, as are 2 and 4.
Vertical angles are congruent.
Example 6:
Use the diagram to find the missing angles.
x = __________
x
87
y
y = ___________
z
z = ___________
Example 7:
What is the value of x in the diagram below?
2x
x
x = ______________
Can you pick out the different
types of angles?
Review:
1. Do two angles have to be adjacent to be
complementary or supplementary?
2. Can vertical angles have a common
side?
3. Can a pair of vertical angles also form a
linear pair?