Download Ch7-Sec7.3

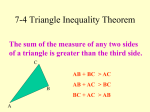
7
THE NATURE OF
GEOMETRY
Copyright © Cengage Learning. All rights reserved.
7.3
Triangles
Copyright © Cengage Learning. All rights reserved.
Terminology
3
Terminology
Every triangle has six parts: three sides and three angles.
We name the sides by naming the endpoints of the line
segments, and we name the angles by identifying the
vertex (see Figure 7.30).
A standard triangle showing the six parts
Figure 7.30
4
Terminology
Triangles are classified both by sides and by angles
(single, double, and triple marks are used to indicate
segments of equal length):
5
Terminology
cont’d
6
Terminology
We say that two triangles are congruent if they have the
same size and shape.
Suppose that we wish to construct a triangle with vertices
D, E, and F, congruent to ABC as shown in Figure 7.30.
A standard triangle showing the six parts
Figure 7.30
7
Terminology
We would proceed as follows (as shown in Figure 7.31):
Constructing congruent triangles
Figure 7.31
1. Mark off segment DE so that it is congruent to AB. We
write this as
2. Construct angle E so that it is congruent to angle B. We
write this as
8
Terminology
3. Mark off segment
You can now see that, if you connect points D and F with a
straightedge, the resulting DEF has the same size and
shape as ABC.
The procedure we used here is called SAS, meaning we
constructed two sides and an included angle (an angle
between two sides) congruent to two sides and an included
angle of another triangle.
We call these corresponding parts.
9
Terminology
There are other procedures for constructing congruent
triangles; some of these are discussed in the problem set.
For this example, we say ABC
DEF.
From this we conclude that all six corresponding parts are
congruent.
10
Example 1 – Corresponding angles with congruent triangles
Name the corresponding parts of the given triangles.
a. ABC ABC 
b. RST UST
Solution:
a.
corresponds to
b.
corresponds to
corresponds to
corresponds to
corresponds to
corresponds to
11
Example 1 – Solution
corresponds to
cont’d
corresponds to
corresponds to
corresponds to
corresponds to
corresponds to
12
Angles of a Triangle
13
Angles of a Triangle
One of the most basic properties of a triangle involves the
sum of the measures of its angles.
14
Example 3 – Use algebra to find angles in a triangle
Find the measures of the angles of a triangle if it is known
that the measures are x, 2x – 15, and 3(x + 7) degrees.
Solution:
Using the theorem for the sum of the measures of angles in
a triangle, we have
x + (2x – 15) + 3(x + 17) = 180
Sum of the measures of the
angles is 180°.
x + 2x – 15 + 3x + 51 = 180
Eliminate parentheses.
6x + 36 = 180
Combine similar terms.
15
Example 3 – Solution
6x = 144
x = 24
cont’d
Subtract 36 from both sides.
Divide both sides by 6.
Now find the angle measures:
x = 24
2x – 15 = 2(24) – 15 = 33
3(x + 17) = 3(24 + 17) = 123
The angles have measures of 24°, 33°, and 123°.
16
Angles of a Triangle
An exterior angle of a triangle is the angle on the other
side of an extension of one side of the triangle.
An example is the angle whose measure is marked as x in
Figure 7.34.
Exterior angle x
Figure 7.34
17
Angles of a Triangle
Notice that the following relationships are true for any
ABC with exterior angle x:
mA + mB + mC = 180° and
mC + x = 180°
Thus,
mA + mB + mC = mC + x
mA + mB = x
Subtract mC from both sides.
18
Angles of a Triangle
19
Example 4 – Find the exterior angle
Find the value of x in Figure 7.35.
What is x?
Figure 7.35
Solution:
=
105 = x
The measure of the exterior angle is 105°.
20
Isosceles Triangle Property
21
Isosceles Triangle Property
In an isosceles triangle, there are two sides of equal length
and the third side is called its base. The angle included by
its legs is called the vertex angle, and the angles that
include the base are called base angles.
There is an important theorem in geometry that is known as
the isosceles triangle property.
22
Isosceles Triangle Property
In other words, if a triangle is isosceles, then the base
angles have equal measures.
The converse is also true; namely, if two angles of a
triangle are congruent, the sides opposite them have equal
length.
23
Example 5 – Equiangular implies equilateral
Give a reasonable argument to prove that if a triangle is
equiangular, it is also equilateral.
Solution:
If ABC is equiangular, then mA = mB = mC Since
mA = mB from the converse of the isosceles triangle
property, we have
Again, since mB = mC, we have
. Thus, we
see that all three sides have the same length, and
consequently ABC is equilateral.
24