Download Lesson 4-3B PowerPoint

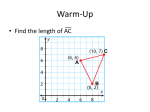
Glencoe Geometry Interactive Chalkboard
Copyright © by The McGraw-Hill Companies, Inc.
Developed by FSCreations, Inc., Cincinnati, Ohio 45202
Send all inquiries to:
GLENCOE DIVISION
Glencoe/McGraw-Hill
8787 Orion Place
Columbus, Ohio 43240
Lesson 4-1 Classifying Triangles
Lesson 4-2 Angles of Triangles
Lesson 4-3 Congruent Triangles
Lesson 4-4 Proving Congruence–SSS, SAS
Lesson 4-5 Proving Congruence–ASA, AAS
Lesson 4-6 Isosceles Triangles
Lesson 4-7 Triangles and Coordinate Proof
Click the mouse button or press the
Space Bar to display the answers.
Example 2 Transformations in the Coordinate Plane
OBJECTIVE: To identify congruent transformations
(2.9.8D) (M8.C.1.1)
COORDINATE GEOMETRY The vertices of RST are
R(─3, 0), S(0, 5), and T(1, 1). The vertices of RST
are R(3, 0), S(0, ─5), and T(─1, ─1). Verify that
RST RST.
Use the Distance Formula to find the length of each side of
the triangles.
Use the Distance Formula to find the length of each side of
the triangles.
Use the Distance Formula to find the length of each side of
the triangles.
Answer: The lengths of the corresponding sides of two
triangles are equal. Therefore, by the definition
of congruence,
Use a protractor to measure the angles of the triangles. You
will find that the measures are the same.
In conclusion, because
,
COORDINATE GEOMETRY The vertices of RST are
R(─3, 0), S(0, 5), and T(1, 1). The vertices of RST 
are R(3, 0), S(0, ─5), and T(─1, ─1). Name the
congruence transformation for RST and RST.
Answer: RST is a
turn of RST.
COORDINATE GEOMETRY The vertices of ABC are
A(–5, 5), B(0, 3), and C(–4, 1). The vertices of ABC
are A(5, –5), B(0, –3), and C(4, –1).
a. Verify that ABC ABC.
Answer:
Use a protractor to verify that
corresponding angles are
congruent.
b. Name the congruence transformation for ABC
and ABC.
Answer: turn
End of Custom Shows
WARNING! Do Not Remove
This slide is intentionally blank and is set to auto-advance to end
custom shows and return to the main presentation.