Download corresponding side of GO

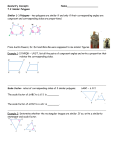
What We Hope You Learn by
the End of this Presentation:
 What is a polygon?
 What are the different types of
polygons?
 What is a congruent polygon?
 What is a similar polygon?
 What are some examples of these
polygons?
A polygon is a plane having three or more
sides.
Convex polygon: all the sides are pushed
outward.
Concave polygon: at least two sides are
pushed inward.
Regular polygon: all the sides have the same
length and their angles are all the same size.
Take a minute to match the
name up with the figure . . .
fact:
Congruent polygons are polygons
that have the same size and the
same shape.
fact:
Congruent shapes have all their
sides and angles congruent.
Notice how the second
figures have the same shape
and size of the first – they
match exactly.
Now we are going to take a
look at similar polygons . . .
Can you find the similar
matches?
Can you find similar polygons?
Same shape
(1) Triangle
(2) Rectangle
Different size
(3) Pentagon
(4) Hexagon
(5) Octagon
Angle does not change
Reduction
Enlargement
Now, let’s define similar !!
Definition:
Figures that have exactly same shape
are called similar figures.
Properties:
(1) In polygons, the size of angles does not change.
(2) One figure is an enlargement or reduction of the
other.
(3) Congruent figures are similar because they have
the same shape.
How can we know the length
of sides in similar figures?
If two figures are similar, one figure is an
enlargement of the other. The size-change
factor tells the amount of enlargement or
reduction.
Example 1: If a copy machine is used to copy a drawing or picture, the
copy will be similar to the original.
Original
Copy
Original
Copy
Original
Copy
Exact Copy
Enlargement
Reduction
Copy machine set to 100%
Copy machine is set to 200%
Copy machine is set to 50%
Size-change factor is 1X
Size-change factor is
2X
Size-change factor is 1 x
2
Example 2: The triangles CAT and DOG are similar. The larger
triangle is an enlargement of the smaller triangle. How long is
side GO?
T
G
2 cm
1.5 cm
? cm
A
3 cm
O
C
3 cm
6 cm
D
Each side and its enlargement
form a pair of sides called
corresponding sides.
(1) Corresponding side of TC -->
GD
(2) Corresponding side of CA-->
DO
(3) Corresponding side of TA-->
GO
Length of
corresponding
sides
GD=3
TC=1.5
DO=6
CA=3
GO=?
TA=2
Ratio of Lengths
3/1.5=2
6/3=2
?/2=2
The size-change factor is 2x.
G
? cm
T
2 cm
3 cm
1.5 cm
O
A
C
3 cm
D
6 cm
(1) Each side in the larger triangle is twice the size of
the corresponding side in the smaller triangle.
(2) Now, let’s find the length of side GO
i) What side is corresponding side of GO? TA
ii) What is the size-change factor? 2X
iii) Therefore, GO= size-change factor x TA
iv) So, GO= 2 x 2 = 4 cm
What we just learned
about similar polygons ?
Not change angle
Different size
Same shape
Similar polygons
Corresponding side
Size-change factor
A polygon is a plane having three or more sides.
Congruent polygons are polygons that have
congruent
congruent
the same size
and the
same shape.
Similar polygons are polygons that have
the samesimilar
shape. similar