Download Lesson

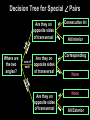
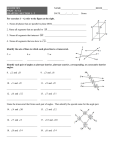
Lesson 3-2
Angles and Parallel Lines
Transparency 3-2
5-Minute Check on Lesson 3-1
Refer to the figure.
1. Name all planes parallel to MNR.
2. Name all segments skew to MP.
Give the special name for each angle pair
in the figure.
3. 1 and 5
4. 3 and 8
5. 4 and 6
6.
How many pairs of alternate interior angles are
there in the figure above?
Standardized Test Practice:
A
1
B
2
C
3
D
4
Transparency 3-2
5-Minute Check on Lesson 3-1
Refer to the figure.
1. Name all planes parallel to MNR. Plane POS (can be
named with any 3 letters from POST)
2. Name all segments skew to MP. TS, QR, NR, OS
Give the special name for each angle pair
in the figure.
3. 1 and 5 corresponding angles
4. 3 and 8 consecutive interior angles
5. 4 and 6 alternate exterior angles
6.
How many pairs of alternate interior angles are
there in the figure above?
Standardized Test Practice:
A
1
B
2
C
3
D
4
Objectives
• Use the properties of parallel lines to
determine congruent angles
• Use algebra to find angle measures
Vocabulary
• No new vocabulary words or symbols
t
Parallel Lines and
Transversals
Postulate/
Theorem
k
3
l
5
7
1 2
4
6
8
Statement
If two parallel lines are cut by a
transversal,
Examples
Corresponding
Angles Post.
then each pair of corresponding angles is
congruent
1  5, 2  6,
3  7, 4  8
Alternate Interior
Angles Thrm
then each pair of alternate interior angles
is congruent
3  6, 4  5
Consecutive Interior
Angles Thrm
then each pair of consecutive interior
angles is supplementary
m3 + m5 = 180°,
m4 + m6 = 180°
Alternate Exterior
Angles Thrm
then each pair of alternate exterior angles
is congruent
1  8, 2  7
Perpendicular
Transversal Thrm
In a plane, if a line is perpendicular to
one of two parallel lines, then it is
perpendicular to the other.
None illustrated
Solving Angle Problems
• 95% of all angle problems are solved by one
of two equations:
– Angle = Angle
– Angle + Angle = 180
(angles are congruent)
(angles are supplementary)
t
k
1
3
Angle = Angle
m1 = m8
3x + 10 = 4x – 30
+30 =
+30
3x + 40 = 4x
-3x
= -3x
40 = x
l
5
7
2
4
Angle + Angle = 180
6
8
m4 + m6 = 180
4x – 30 + x + 10 = 180
5x – 20 = 180
+20 = +20
5x = 200
x = 40
In the figure x || y and
m11 = 51. Find m16.
Corresponding Angles Postulate
Vertical Angles Theorem
Transitive Property
Definition of congruent angles
Substitution
Answer:
In the figure, a || b and m18 = 42. Find m19 and m 25
Answer: m19 = 138, and m25 = 42
What is the measure of RTV?
You need to find RTV. Be sure to identify it correctly on
the figure. Look for patterns!!
Solve the Test Item
Alternate Interior
Angles Theorem
Definition of congruent angles
Substitution
Alternate Interior Angles Theorem
Definition of congruent angles
Substitution
Angle Addition Postulate
What is the measure of IGE?
Answer: 93
ALGEBRA If
and
find x and y.
Find x.
by the Corresponding Angles
Postulate.
Definition of congruent angles
Substitution
Subtract x from each side and
add 10 to each side.
Find y.
by the Alternate Exterior Angles
Theorem.
Definition of congruent angles
Substitution
Substitution
Simplify.
Add 100 to each side.
Divide each side by 4.
Answer:
ALGEBRA: If m1 = 9x + 6, m2 = 2(5x – 3), and
m3 = 5y + 14, find x and y.
Answer: x = 12 and y = 20
Decision Tree for Special  Pairs
Are they on
opposite sides
of transversal
Where are
the two
angles?
one of
each
Are they on
opposite sides
of transversal
Are they on
opposite sides
of transversal
Consecutive Int
Alt Interior
Corresponding
None
None
Alt Exterior
Identification: Determine what each of these angle
pairs are in the drawing below:
Acute Angle:
Alternate Interior Angles:
9
5 11
13 14 8
6 12
10
4 16 15 7
Alternate Exterior Angles:
Corresponding Angles:
Consecutive Interior Angles:
Linear Pair of Angles:
Obtuse Angle:
Right Angle:
Vertical Angle Pair:
Answer: many combinations are possible
ALGEBRA: If m4 = 2x + 16 and m4 = 2(4x – 3),
find m1, and m4.
4
Answer: m1 = 130° m4 = 50°.
ALGEBRA: If m1 = 9x + 6, m2 = 2(5x – 3), and
m3 = 5y + 14, find m1, m2, m3, and m4.
4
Answer: m1 = 114°, m2 = 114°,
m3 = 114°, and m4 = 66°.
Summary & Homework
• Summary:
– Pairs of congruent angles formed by parallel lines
and a transversal are corresponding angles,
alternate interior angles and alternate exterior
angles
– Pairs of consecutive interior angles are
supplementary
• Homework:
– Day 1: pg 136 – 137: 1, 5-11, 14-19
– Day 2: pg 136 – 137: 20-25, 26, 27, 29, 31, 39