Download 13.2 Angles of Rotation

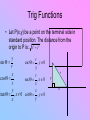
13.2 Angles of Rotation
Unit Circle Quiz: May 11
Ch. 13 Test: May 13
Do you recall…
• In geometry, an angle is defined by two rays that
have a common endpoint.
• In trig, an angle is defined by a ray that is rotated
around the endpoint…this is called ANGLE OF
ROTATION.
– The Greek letter theta, Θ, is commonly used to name
an angle of rotation.
• The starting position is the Initial Side and the
final position is the TERMINAL SIDE.
• When the endpoint is at the origin, it is called
STANDARD POSITION.
What else?
• If rotated COUNTERCLOCKWISE- the
angle has a positive measure
• If rotated CLOCKWISE-the angle has a
negative measure
• The most common unit for angle measure
is the degree.
• A complete rotation is 360 degrees, so 45
degrees is 1/8th of a complete rotation.
– (hint…divide)
COTERMINAL
• Two angles are co-terminal if they have
the same terminal side.
– What is co-terminal with 230 degrees?
• You can find the co-terminal angles by adding or
subtracting integer multiples of 360o.
Example:
• Find the coterminal angle, θ, for each
angle below such that -360o<θ<360o.
 180o
 -27o
Reference Angles
• For an angle in standard position, the
reference angle, Θref , is the positive
acute angle formed by the terminal side
and the x-axis.
Example:
• Find the reference angle for:
 94 degrees
 245 degrees
 290 degrees
 -110 degrees
Trig Functions
• Let P(x,y) be a point on the terminal side in
standard position. The distance from the
origin to P is: x 2  y 2
y
r
sin  
csc   , y  0
r
y
x
r
cos  
sec   , x  0
r
x
x
y
tan   , x  0 cot   , y  0
y
x
r
y
x
Example:
• Let P(-2,-3) by a point on the terminal side
in standard position. Find the exact values
of the 6 trig functions.
Let’s make you think…
• The terminal side of Θ in standard form is
in Quadrant II and cos Θ = -3/5. Find the
exact values of the 6 trig functions.
Practicing Helps You Remember
• P. 841 #9 – 63 odd