Download 3.2 Proof and Perpendicular Lines

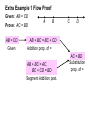
PROOF AND PERPENDICULAR
LINES
3.2
GOAL
1
COMPARING TYPES OF PROOFS
Vocabulary
•two-column proof
•paragraph proof
•flow proof
EXAMPLE 1
Be sure you identify the
similarities and differences in the
three types of proof.
Note that the statements and
reasons are the same, but are
written in a different form.
Extra Example 1
Given: AB = CD
Prove: AC = BD
Statements
A
B
C
D
Reasons
1. AB = CD
1. Given
2. AB + BC = BC + CD
2. Addition prop. of =
3. AB + BC = AC and
BC + CD = BD
3. Segment Addition post.
4. AC = BD
4. Substitution prop. of =
Now use your two-column proof
to write a paragraph proof.
Extra Example 1 Paragraph Proof
Given: AB = CD
Prove: AC = BD
A
B
C
D
Because AC = BD, the addition property of equality says
that AB + BC = BC + CD. Since AB + BC = AC and
BC + CD = BD by the segment addition post., it follows
from the substitution prop. of equality that AC = BD.
Now write a flow proof.
Extra Example 1 Flow Proof
Given: AB = CD
Prove: AC = BD
AB = CD
Given
A
B
C
D
AB + BC = BC + CD
Addition prop. of =
AB + BC = AC,
BC + CD = BD
Segment Addition post.
AC = BD
Substitution
prop. of =
PROOF AND PERPENDICULAR
LINES
3.2
GOAL
2
PROVING RESULTS ABOUT
PERPENDICULAR LINES
THEOREMS ABOUT PERPENDICULAR LINES
3.1 If two lines intersect to form a linear pair of congruent
angles, then the lines are perpendicular.
3.2 If two sides of two adjacent angles are perpendicular,
then the angles are complementary.
3.3 If two lines are perpendicular, then they intersect to
form four right angles.
EXAMPLE 2
Extra Example 2
Write a two-column proof of Theorem 3.2.
A
Given: BA  BC
Prove: 1 and 2 are complementary.
Statements
2 1
B
Reasons
1. BA  BC
1. Given
2. ABC is a right angle.
2. Def. of  lines
3. mABC  90
3. Def. of right s
4. m1 m2  mABC
4.  Addition Post.
5. m1 m2  90
5.
Subs. Prop. of =
6. 1 and 2 are complementary. 6. Def. of comp. s
C
Checkpoint
Use the following to write a paragraph proof of the
Congruent Supplements Theorem.
Given: 2  4
1 is supplementary to 2.
3 is supplementary to 4.
1
2
Prove:
3
A solution is on the next slide.
4
1  3
Checkpoint Solution
Since 1 is supplementary to 2 and 3 is supplementary
to 4, m1 m2  180 and m3  m4  180 by the
definition of supplementary angles. Therefore the symmetric
and transitive properties of equality say that m1  m2 
m3  m4. It is given that 2  4, so by the definition
of congruent angles, m2  m4. The subtraction property
of equality allows the statement m1  m3. Finally, by the
definition of congruent angles,
1  3.
QUESTIONS?