Download quad - mgriffi4

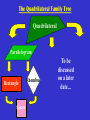
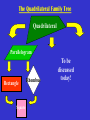
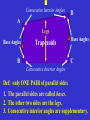
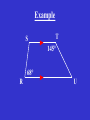
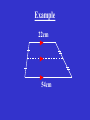
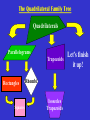
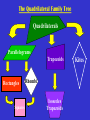
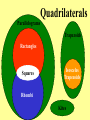
The Quadrilateral
Family Tree
Created by Tony McCullers, Edited by Mindy Griffis
M4G1. Students will define and identify the characteristics of geometric
through examination and construction.
c. Examine and classify quadrilaterals (including parallelograms, squares,
rectangles, trapezoids, and rhombi).
d. Compare and contrast the relationships among quadrilaterals.
QCC - Euclidean Geometry (10th grade)
#19 States and applies properties of triangles and quadrilaterals such as
parallelograms, rectangles, rhombi, squares, and trapezoids.
# 21 Uses properties of quadrilaterals to establish and test relationships involving
diagonals, angles, and lines of symmetry.
Quadrilateral
Def: 4 sides, 4 vertices
A + B + C + D = 360°
Parallelogram
Def: opposite sides are parallel
1.
2.
3.
4.
The opposite sides are congruent.
The opposite angles are congruent.
The consecutive angles are supplementary.
The diagonals bisect each other.
Rectangle
1. Have four right angles.
2. The diagonals are congruent.
1. All 4 sides are
congruent.
Rhombus
2. The diagonals are
perpendicular.
3. The diagonals bisect
the angles.
Rhombi
Rectangles
Squares
A square has all of the properties
of Rectangles and Rhombi!
The Quadrilateral Family Tree
Quadrilateral
Parallelogram
Rectangle
Square
Rhombus
To be
discussed
on a later
date…
Examples
Decide whether the statement is true
ALWAYS, SOMETIMES, or NEVER .
1. A rectangle is a square
SOMETIMES
2. A square is a rhombus.
ALWAYS
3. A rectangle is a parallelogram
ALWAYS
Examples
4. QRST is a square. What else do you
know about QRST?
5. EFGH is a rectangle. K is the
midpoint of FH. FH = 10. (Draw it!)
- Find KF.
- Find EG.
- Find EK.
GO TO PAGE 351.
Page 351
1. Equilateral Quadrilateral
Rhombus or Square
7. All sides are congruent
Rhombus or Square
8. All angles are congruent
Square, Rectangle
9. Diagonals are congruent
Square, Rectangle
10. Opposite angles are congruent
Parallelogram, Rectangle, Rhombus, Square
HOMEWORK:
P. 351 (#16 – 38 even)
Only 12 problems.
The Quadrilateral Family Tree
Quadrilateral
Parallelogram
Rectangle
Square
Rhombus
To be
discussed
today!
Consecutive Interior Angles
D
A
Legs
Base Angles
Trapezoids
B
Base Angles
C
Consecutive Interior Angles
Def: only ONE PAIR of parallel sides
1. The parallel sides are called bases.
2. The other two sides are the legs.
3. Consecutive interior angles are supplementary.
Example
S
T
145°
68°
R
U
Midsegment of a Trapezoid
Def: a segment that joins
the midpoints of the
Trapezoid’s legs.
Length of Midsegment = ½ (Base+Base)
Example
22cm
54cm
Isosceles
Trapezoids
1. The legs are congruent.
2. Each pair of base angles are congruent.
3. Diagonals are congruent!
Example
CDEF is an isosceles trapezoid with
CE=10 and E=95°. Find DF. Find the
measure of angles C, D, and F.
C
D
F
E
Go to Page 359
Homework: p.359 (10 - 24 even)
The Quadrilateral Family Tree
Quadrilaterals
Parallelograms
Trapezoids
Rectangles
Squares
Rhombi
Isosceles
Trapezoids
Let’s finish
it up!
NO PAIRS OF PARALLEL SIDES!
A
D
Kites
Def: two pairs of consecutive
sides that are congruent, but
opposite sides are not
B
congruent.
1) Exactly one pair of opposite
angles are congruent.
C
2) The diagonals are
perpendicular.
Example
80°
126°
100°
Example
K
3
H
4
4
J
Given: HIJK is a kite.
Find the measure of
each side.
KH = 5
7
KJ = 5
HI = 8.1
I
JI = 8.1
The Quadrilateral Family Tree
Quadrilaterals
Parallelograms
Trapezoids
Rectangles
Squares
Rhombi
Isosceles
Trapezoids
Kites
Go to page 360
• Do # 28 and 32
#28 Find AB=AD = ? And CB=CD=?
#32 Find mH and m G.
Quadrilaterals
Parallelograms
Trapezoids
Rectangles
Squares
Isosceles
Trapezoids
Rhombi
Kites