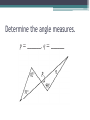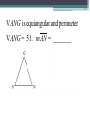Download Unit 2 Review

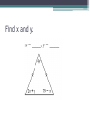
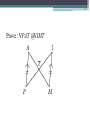
Unit 2 – Triangles
Review for Final Exam
True/False
• A scalene triangle is a triangle with no two sides
the same length.
True/False
• An obtuse triangle is a triangle that has one
angle measuring greater than 90°.
True/False
• An isosceles right triangle is a triangle with an
angle measuring 90° and no two sides
congruent.
True/False
• If the base angles of an isosceles triangle each
measure 48°, then the vertex angle has a
measure of 132°.
True/False
• If a triangle has two angles of equal measure,
then the triangle is equilateral.
True/False
• If a triangle has two angles of equal measure,
then the third angle is acute.
True/False
• If two sides of a triangle measure 45 cm and 36
cm, then the third side must be greater than 9
cm and less than 81 cm.
True/False
• The sum of the measures of the three angles of
an obtuse triangle is greater than the sum of the
measures of the three angles of an acute triangle.
True/False
• The incenter, the centroid, and the circumcenter
are always inside the triangle.
True/False
• An altitude of a triangle must be inside the
triangle.
True/False
• The orthocenter of a triangle is the point of
intersection of the three perpendicular bisectors
of the sides.
True/False
• If TR is a median of VTIE and point D is the
centroid, then TD = 3DR.
True/False
• The incenter of a triangle is the point of
intersection of the three angle bisectors.
Always/Sometimes/Never
• If a triangle is a right triangle, then the acute
angles are complementary.
Identify the point of concurrency.
• A stained-glass artist wishes to circumscribe a
circle about a triangle in her latest abstract
design.
Identify the point of concurrency.
• Rosita wants to install a circular sink in her new
triangular countertop. She wants to choose the
largest sink that will fit.
Identify the point of concurrency.
• Julian Chive wishes to center a butcher-block
table at a location equidistant from the
refrigerator, stove, and sink.
Identify the point of concurrency.
• The first-aid center of Mt. Thermopolis State
Park needs to be at a point that is equidistant
from three bike paths that intersect to form a
triangle.
Determine the angle measures.
Find x and y.
V ANG is equiangular and perimeter
V ANG = 51. mAN = _______
Name the conjecture that leads to this
congruence statement.
Prove : VPAT @VIMT
Given : TS bisects MA, MT @ AT
Prove :VMST @V AST
Given : V ABC is isosceles and CDis the bisector of the vertex angle.
Prove : AD @ BD