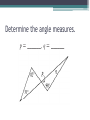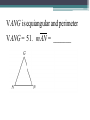* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Unit 2 Review
Golden ratio wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
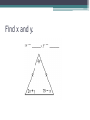
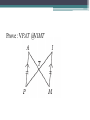
Unit 2 – Triangles Review for Final Exam True/False • A scalene triangle is a triangle with no two sides the same length. True/False • An obtuse triangle is a triangle that has one angle measuring greater than 90°. True/False • An isosceles right triangle is a triangle with an angle measuring 90° and no two sides congruent. True/False • If the base angles of an isosceles triangle each measure 48°, then the vertex angle has a measure of 132°. True/False • If a triangle has two angles of equal measure, then the triangle is equilateral. True/False • If a triangle has two angles of equal measure, then the third angle is acute. True/False • If two sides of a triangle measure 45 cm and 36 cm, then the third side must be greater than 9 cm and less than 81 cm. True/False • The sum of the measures of the three angles of an obtuse triangle is greater than the sum of the measures of the three angles of an acute triangle. True/False • The incenter, the centroid, and the circumcenter are always inside the triangle. True/False • An altitude of a triangle must be inside the triangle. True/False • The orthocenter of a triangle is the point of intersection of the three perpendicular bisectors of the sides. True/False • If TR is a median of VTIE and point D is the centroid, then TD = 3DR. True/False • The incenter of a triangle is the point of intersection of the three angle bisectors. Always/Sometimes/Never • If a triangle is a right triangle, then the acute angles are complementary. Identify the point of concurrency. • A stained-glass artist wishes to circumscribe a circle about a triangle in her latest abstract design. Identify the point of concurrency. • Rosita wants to install a circular sink in her new triangular countertop. She wants to choose the largest sink that will fit. Identify the point of concurrency. • Julian Chive wishes to center a butcher-block table at a location equidistant from the refrigerator, stove, and sink. Identify the point of concurrency. • The first-aid center of Mt. Thermopolis State Park needs to be at a point that is equidistant from three bike paths that intersect to form a triangle. Determine the angle measures. Find x and y. V ANG is equiangular and perimeter V ANG = 51. mAN = _______ Name the conjecture that leads to this congruence statement. Prove : VPAT @VIMT Given : TS bisects MA, MT @ AT Prove :VMST @V AST Given : V ABC is isosceles and CDis the bisector of the vertex angle. Prove : AD @ BD