Download Solve for x

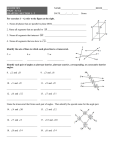
Bellwork: Thursday May 17th
Solve for x and then find the
measure of each angle
Solve for x
8x – 8 = 7x + 3
8x – 8 = 7x + 3
-7x
-7x
1x – 8 = 3
+8 +8
1x = 11
÷1 ÷ 1
x = 11
Set
both
values
equal to
each
other
Solve
for x
Bellwork Continued: Use x to find the measure of
the angles
8  11 – 8
Step 1: Solve for x
x = 11
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 80°
Angle 2 = 80°
7  11 + 3
Step 4: Check to see that both
angles have the same measure
80° = 80°
Homework Answers
Angle 1 = 135˚
Angle 2 = 135˚
Angle 1 = 50˚
Angle 2 = 50˚
Angle 1 = 46˚
Angle 2 = 46˚
Angle 1 = 90˚
Angle 2 = 90˚
Angle 1 = 130˚
Angle 2 = 130˚
Angle 1 = 68˚
Angle 2 = 68˚
Angle 1 = 119˚
Angle 2 = 119˚
Angle 1 = 60˚
Angle 2 = 60˚
Solve for x and then find
the measure of each
angle for x
Solve for x
9x + 2 = 10x – 10
9x + 2 = 10x – 10
-10x
-10x
-1x + 2= -10
- 2 -2
-1x = -12
÷-1 ÷ -1
x = 12
Set
both
values
equal
to each
other
Solve
for x
Use x to find the measure of the angles
9  12 + 2
Step 1: Solve for x
x = 12
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 110°
Angle 2 = 110°
10  12 –
10
Step 4: Check to see that both
angles have the same measure
110° = 110°
Match the following words with the correct
definition.
1.
2.
3.
4.
5.
Complementary
Supplementary
Alternate Exterior Angles
Alternate Interior Angles
Corresponding Angles
A. Angles in the same location
on two different parallel
lines cut by a transversal
B. Angles whose sum is 180°
C. Angles whose sum is 90°
D. Two non-adjacent angles
inside two parallel lines cut
by a transversal
E. Two non-adjacent angles
outside two parallel lines
cut by a transversal
•Two angles whose sum
equals 90° are called what?
Find the value of x by writing and solving
an equation
Find the value of x by writing and solving
an equation.
Find the value of x and then find the
measure of each angle
Solve for x
22x + 10 + 58 = 90
22x + 68 = 90
- 68 -68
2x = 22
÷2 ÷2
x = 11
Use x to find the
measure of the
angles
Step 1: Solve for x
x = 11
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 58°
Angle 2 = 32°
Step 4: Check to see that the angles
add up to 90° or 180 °
58° + 32° = 90°
Find the value of x and then find the
measure of each angle
Solve for x
5x + 1 + 3x + 9 = 90
8x + 10 = 90
- 10 -10
8x = 80
÷8 ÷8
x = 10
Use x to find the
measure of the
angles
Step 1: Solve for x
x = 10
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 39°
Angle 2 = 51°
Step 4: Check to see that the angles
add up to 90° or 180 °
39° + 51° = 90°
•Two angles whose sum
equals 180° are called what?
Find the value of x by writing and solving
an equation
Find the value of x by writing and solving
an equation
Find the value of x and then find the
measure of each angle
Solve for x
2x + 28 + 92 = 180
2x + 120 = 180
- 120 -120
2x = 60
÷2 ÷2
x = 30
Use x to find the
measure of the
angles
Step 1: Solve for x
x = 30
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 88°
Angle 2 = 92°
Step 4: Check to see that the angles
add up to 90° or 180 °
88° + 92° = 180°
Find the value of x and then find the
measure of each angle
Solve for x
x + 3 + 4x + 2 = 180
5x + 5 = 180
- 5 -5
5x = 175
÷5 ÷5
x = 35
Use x to find the
measure of the
angles
Step 1: Solve for x
x = 35
Step 2: Plug the “x” value into both
angles
Step 3: Find the value of the two
angles
Angle 1 = 38°
Angle 2 = 142°
Step 4: Check to see that the angles
add up to 90° or 180 °
38° + 142° = 180°
• What do you call congruent
angles that are on the inside
of the parallel lines but on
opposite sides of the
transversal?
• What do you call congruent
angles that are on the
outside of the parallel lines
but on opposite sides of the
transversal?
Find the value of two unknown angles
Find the value of two unknown angles
Find the value of two unknown angles
Find the value of two unknown angles
Find the value of x and then find the
measure of each angle
Solve for x
16x – 8 = 8 + 14x
-14x
-14x
2x – 8 = 8
+8 +8
2x = 16
÷2 ÷2
x=8
Find the value of x and then find the
measure of each angle
Substitute x with 8 then
simplify
16x – 8
and 8 + 14x
16(8) – 8
and
8 + 14(8)
120˚
Find the value of x and then find the
measure of each angle
Solve for x
17x + 3 = 105
-3
-3
17x = 102
÷17 ÷ 17
x=6
Find the value of x and then find the
measure of each angle
Substitute x with 6 then
simplify
17 x + 3 and 105°
17(6) + 3 and
105°
105˚
•What do you call
congruent angles in the
same location on two
different parallel lines cut
by a transversal?
Find the value of x and then find the
measure of each angle
Solve for x
7x – 10 = 5x + 10
-5x
-5x
2x – 10 = 10
+ 10 + 10
2x = 20
÷2 ÷2
x = 10
Find the value of x and then find the
measure of each angle
Substitute x with 10 then
simplify
7x – 10 and 5x + 10
7(10) – 10 and
5(10) + 10
60˚
Find the value of x and then find the
measure of each angle
Solve for x
11x – 6 = 10x
-11x
-11x
-6 = -1x
÷-1 ÷-1
x=6
Find the value of x and then find the
measure of each angle
Substitute x with 6 then
simplify
10x
and 11x – 6
10(6)
and
11(6) – 6
60˚
Homework
• Review worksheet.
• Remember…Quiz tomorrow.