Download SAT MATH PREPERATION

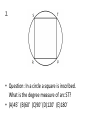
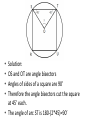
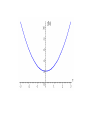
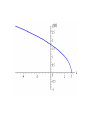
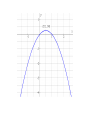
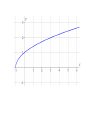
SAT MATH PREPERATION
Problems Related to SAT
•
•
•
•
Geometry
Algebra
Precalculus
Additional problems in the blog
Problems
1.
• Question: In an isosceles triangle ABC, AM &
CM are angle bisectors of angles BAC and BCA
respectively. What is the measure of angle
AMC?
• (A)110’ (B)115’ (C)120’ (D)125’ (E)130’
• Solution:
• Isosceles triangle means that any 2 sides are
equal
• Here we consider AB and CB to be equal
• Therefore angles BAC and BCA are equal and
the value is (180-40)/2 = 70’
• We are given that AM and CM are angle
bisectors. Angles MAC and MCA = 35’
• Finally angle AMC is 180-(2*35) = 110’
2.
• Question: In a circle a square is inscribed.
What is the degree measure of arc ST?
• (A)45’ (B)60’ (C)90’ (D)120’ (E)180’
•
•
•
•
Solution:
OS and OT are angle bisectors
Angles of sides of a square are 90’
Therefore the angle bisectors cut the square
at 45’ each.
• The angle of arc ST is 180-(2*45)=90’
3. 5/x = (5 + a)/(x + a) ; If a not equal to 0, find
the value of x?
• (A)-5 (B)-1 (C)1 (D)2 (E)5
• Solution:
• Multiply x on both sides to get
5 = (5 + a)*x/(x + a)
• Multiply (x + a) on both sides to get
5(x + a) = x*(5 + a)
• Simplify to get 5x + 5a = 5x + x*a
• 5a – x*a = 0
• a(5 - x) = 0
• Given that a is not zero. Therefore (5 - x)=0
• This implies x = 5
4. If y = 2x + 3 and x < 2 which of the following
represents all possible values of y?
• (A)y<7 (B)y>7 (C)y<5 (D)y>5 (E)5<y<7
• Solution:
• Consider that x = 2
• Substitute the value of x in main equation to
get the value of y
• y = 2*2 + 3 = 7
• Since x is less than 2 therefore y must be less
that 7.
• y<7
5. Let the function f(x) = 5x – 2a, where a is a
constant. If f(10) + f(5) = 55, what is the value
of a?
• (A)-5 (B)0 (C)5 (D)10 (E)20
• Solution:
• f(10) = 5*10 – 2a = 50 – 2a
• f(5) = 5*5 – 2a = 25 – 2a
• Substitute in the above results in the Given
function f(10) + f(5) = 55
• 50 – 2a + 25 – 2a = 55
• -4a = -20
•
a=5
6. If f(x) = 2x and g(x) = x + 2. Find the answer for
fog(x)?
• (A)2x + 4 (B)x + 2 (C)2x + 2 (D)3x + 2 (E)x + 2
• Solution:
• The above problem is a function within function
• fog(x) means f(g(x)). This means we substitute
the value of g(x) in place of the x term in the f(x)
equation
• We get f(x + 2) = 2(x + 2) = 2x + 4
Extra Problems in the blog
• The following problems have the solutions
also being provided
1. Given that x + k = 6 and p(x + k) = 36. Find the
value of p?
• (A)8 (B)6 (C)-8 (D)-6 (E)-2
• Solution:
• Given that (x + k) = 6
• Substitute this value in the second equation
• p * 6 = 36
• Therefore p = 6
2. y = h/x ; h is a constant. Initially the value of y
is 3 and x is 4. Find the value of y when x is 6?
• (A)-2 (B)5 (C)-1 (D)1 (E) 2
• Solution:
• We find the value of h by substituting values
of y = 3 and x = 4 in the main equation
• We get h = 4 * 3 = 12
• Now we find y = h/x = 12/6 = 2
3. A rectangle is 4 times as long as it is wide. If
the length is increased by 4 inches and the
width is decreased by 1 inch, the area will be
60 square inches. What were the dimensions
of the original rectangle?
• Solution:
• Draw a rectangle with the required
dimensions
• Let x = original width of rectangle
• Area of rectangle = Length * Width
• Plug in the values from the question and from the
sketch 60 = (4x + 4)(x –1)
• Solving we get 4x2 – 4 – 60 = 0
(2x – 8)(2x + 8) = 0
x= 4 or x = -4
• We consider only the positive value. So the width
of the original rectangle is 4 and the length is 16
4. Find the domain and range for function
f(x) = x2 + 2.
• Solution:
• The function f(x) = x2 + 2 is defined for all real
values of x.
• Therefore the domain is all real values of x
• Since x2 is never negative, x2 + 2 is never less
than 2. Hence, the range of f(x) is "all real
numbers f(x) ≥ 2".
5. Find the domain and range for the function
• Solution:
• g(s) is not defined for real numbers greater
than 3 which would result in imaginary no.
• Hence, the domain for g(s) is "all real
numbers, s ≤ 3".
• Also
>= 0. The range of g(s) is
"all real numbers g(s) ≥ 0"
6. Graph the function y = x − x2
• Solution:
• Determine the y-values for a typical set of xvalues and write them in a table.
• Plot the values on a x-y plane.
• For a better graph have more number of
points
7. Graph the function
• Solution:
• Note: y is not defined for values of x < -1
• We determine x and its corresponding yvalues and write them in a table
• Draw the graph
8. Consider the function
• Solution:
• Factoring the denominator gives
• We observe that the function is not
defined for x = 0 and x = 1.
• Here is the graph of the function.
• We say the function
is discontinuous when x = 0 and x = 1.