Download 6.4_Rectangles_(web)

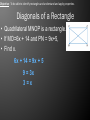
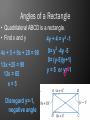
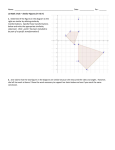
"Are you really sure that a floor can't also be a ceiling?" M.C. Escher
Rectangles
•
•
•
•
•
A rectangle is a quadrilateral with four right angles.
A rectangle is a parallelogram.
A rectangle has opposite congruent sides.
Diagonals of a rectangle bisect each other.
The diagonals of a rectangle are congruent.
If the diagonals of a parallelogram are congruent, then the
parallelogram is a rectangle.
6.4 Rectangles
Check.3.2 Connect coordinate geometry to geometric figures in the
plane (e.g. midpoints, distance formula, slope, and polygons).
Spi.3.2 Use coordinate geometry to prove characteristics of
polygonal figures.
Check.4.10 Identify and apply properties and relationships of
special figures (e.g., isosceles and equilateral triangles, family of
quadrilaterals, polygons, and solids).
"Are you really sure that a floor can't also be a ceiling?" M.C. Escher
Rectangles
•
•
•
•
•
A rectangle is a quadrilateral with four right angles.
A rectangle is a parallelogram.
A rectangle has opposite congruent sides.
Diagonals of a rectangle bisect each other.
The diagonals of a rectangle are congruent.
If the diagonals of a parallelogram are congruent, then the
parallelogram is a rectangle.
Objective: To be able to identify rectangles and understand and apply properties.
Diagonals of a Rectangle
• Quadrilateral MNOP is a rectangle.
• If MO=6x + 14 and PN = 9x+5,
• Find x.
6x + 14 = 9x + 5
9 = 3x
3=x
Angles of a Rectangle
• Quadrilateral ABCD is a rectangle.
• Find x and y
4y + 4 = y2 -1
4x + 5 + 9x + 20 = 90
13x +25 = 90
13x = 65
x=5
Disregard y=-1,
negative angle
0= y2 -4y -5
0= (y-5)(y+1)
y = 5 or y=-1
Coordinate Plane
Determine if Quadrilateral FGHJ
is a rectangle given vertices at
F(-4, -1), G(-2, -5), H(4, -2), J(2,2)
Perpendicular lines form Right Angles
Slopes of perpendicular lines are opposite inverses
Sides consecutive
sides are
perpendicular
making this a
rectangle.
Also could have
used distance
formula
Summary
• Rectangle is a special parallelogram which is a
special quadrilateral.
• Rectangle has all the properties of a parallelogram
• Plus in a rectangle all angles are right angles and
the diagonals of a rectangle are congruent.
• Practice Assignment
– Page 422, 10 - 30 even