Download Labor

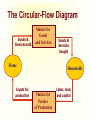
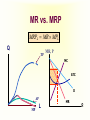
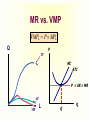
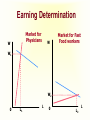
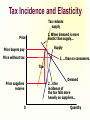
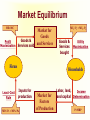
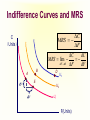
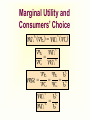
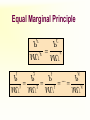
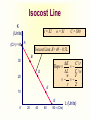
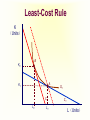
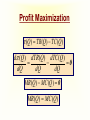
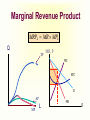
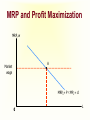
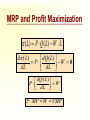
Principles of Economics
Session 9
Topics To Be Covered
Demand for Labor
Marginal Revenue Product
Supply of Labor
Labor Market Equilibrium
Earning Determination
Rent
Return on Capital
Inequality of Income Distribution
Topics To Be Covered
General Equilibrium
Pareto Efficiency
Production Possibilities Frontier
Externalities
Production and Distribution
The Circular-Flow Diagram
Goods &
Services sold
Market for
Goods
and Services
Firms
Inputs for
production
Goods &
Services
bought
Households
Market for
Factors
of Production
Labor, land,
and capital
Factors of Production
Factors of production are the
inputs used to produce goods
and services.
Factors of Production
Capital
(Physical Capital)
Labor (Human Capital)
Land (Natural Resources)
Technological Knowledge
The Market for the Factors
of Production
The demand for a factor of
production is a derived demand.
A firm’s demand for a factor of
production is derived from its
decision to supply a good in
another market.
The Demand for Labor
Labor markets, like other markets
in the economy, are governed by the
forces of supply and demand.
The Versatility of
Supply and Demand
The Market for Apples
The Market for Apple Pickers
Price of
Apples
Wage of
Supply Apple
Pickers
P
W
Supply
Demand
Demand
0
Q
Quantity
of Apples
0
L
Quantity of
Apple Pickers
The Demand for Labor
Most labor services, rather than
being final goods ready to be enjoyed
by consumers, are inputs into the
production of other goods.
Production Function and
Marginal Product of Labor
The production function illustrates the
relationship between the quantity of
inputs used and the quantity of output
of a good.
Production Function
with One Variable Input (Labor)
Amount
Amount
Total
Average
of Labor (L) of Capital (K) Output (Q) Product
Marginal
Product
0
10
0
---
---
1
10
10
10
10
2
10
30
15
20
3
10
60
20
30
4
10
80
20
20
5
10
95
19
15
6
10
108
18
13
7
10
112
16
4
8
10
112
14
0
The Law of Diminishing
Marginal Product
Total Product
Output
per
Month
The Law of Diminishing
Marginal Product
Average Product
0 1
2
3 4
5 6
7
9
Labor per Month
Marginal Product
The Law of Diminishing
Marginal Product
The Law of Diminishing Marginal
Product states that the marginal
product (MP) of an input declines as
the quantity of the input increases.
Marginal Revenue Product
 The marginal revenue product (MRP) is the
extra revenue that would be brought in if a firm
were to buy one extra unit of an input, put it to
work, and sell the extra product it produced.
 In the perfectly competitive market, the
marginal revenue equals the price, MRP is also
called value of marginal product (VMP).
Marginal Revenue Product
MRPL  MR  MPL
VMPL  P  MPL
MR vs. MRP
The MR is the change of total
revenue resulting from increasing
one more unit of product, while the
MRP is the change of total revenue as
a result of adding an extra unit of
production factor.
MR vs. MRP
MRPL  MR  MPL
Q
TP
MR, P
MC
ATC
D
AP
MP
L
MR
Q
MR vs. VMP
VMPL  P  MPL
Q
P
TP
MC
ATC
P = AR = MR
AP
MP
L
Q
Q
MRP of Labor
L
TP
AP
MP
MR
MRP
3
60
20
30
3
90
4
80
20
20
3
60
5
95
19
15
3
45
6
108
18
13
3
39
7
112
16
4
3
12
MRP of Labor
MRPL
($)
90
MRP
L
0
1
2
3
4
5
6
7
8
9
L
MRP of Labor
 The
MRP is measured in dollars.
 It diminishes as the number of
workers rises because the MP is
decreasing and the market price of
the good is constant.
MRP and
the Demand for Labor
To maximize profit, the competitive,
profit-maximizing firm hires workers up
to the point where the MRP equals the
wage—the marginal factor cost (MFC).
MRP  MFC
MRPL  w
MRP and
the Demand for Labor
The MRP curve is the
labor demand curve for a profitmaximizing firm.
MRP and
the Demand for Labor
MRP
Competitive Output Market(P=MR)
Market
wage
B
A
Monopolistic
Output Market
(P＞MR)
MRPL= MR ×MPL = d
0
MRPL= P×MPL = d
L
MRP and
the Demand for Labor
If MRPL > w,
hire more labor.
If MRPL < w,
hire less labor.
If MRPL = w,
it is a profit maximizing amount of labor
What Causes the Labor
Demand Curve to Shift?
 Output
price
 Technological change
 Supply of other factors
The Supply of Labor
The market supply for physical
inputs is upward sloping.
The market supply for labor may be
upward sloping and backward
bending.
The Supply of Labor
The choice to supply labor is based on
utility maximization.
Leisure competes with labor for utility.
Wage rate measures the price of leisure.
Higher wage rate causes the opportunity
cost of leisure to increase.
The Supply of Labor
The Substitution Effect
Higher wages encourage workers to substitute
work for leisure.
The Income Effect
Higher wages allow the worker to purchase
more goods. Even if they work less, they may
maintain their previous living standard.
The Backward Bending Supply Curve.
If the income effect exceeds the substitution
effect, the supply curve is backward bending.
Backward-Bending Supply
of Labor
Wage
($ per
hour)
Income Effect ＞
Substitution Effect
Income Effect ＜
Substitution Effect
Supply of Labor
Hours of Work per Day
What Causes the Labor
Supply Curve to Shift?
 Changes
in tastes
 Changes in alternative opportunities
 Immigration
Labor Market Equilibrium
Wage
(price of
labor)
Supply
Equilibrium
wage, W
Demand
0
Equilibrium
employment, L
Quantity of
Labor
Labor Market Equilibrium
Labor supply and labor demand
determine the equilibrium wage.
Shifts in the supply or demand
curve for labor cause the
equilibrium wage to change.
Equilibrium in a
Competitive Output Market
 DL(MRPL)
= SL
w = MRPL
 MRPL = P×MPL
 Markets are efficient.

Equilibrium in a
Competitive Output Market
 MR
<P
 MRP L= MR×MPL
 w = MRPL
 Using less than the efficient level of
input
Productivity and Wage
Growth around the World
Growth Rate
Growth Rate
of Real
Country
of Productivity
Wages
South Korea
8.5
7.9
Hong Kong
5.5
4.9
Singapore
5.3
5.0
Indonesia
4.0
4.4
Japan
3.6
2.0
India
3.1
3.4
United Kingdom
2.4
2.4
United States
1.7
0.5
Brazil
0.4
-2.4
Mexico
-0.2
-3.0
Argentina
-0.9
-1.3
Iran
-1.4
-7.9
Differences in Earnings in
the U.S. Today
 The
typical physician earns about
$200,000 a year.
 The typical police officer earns about
$50,000 a year.
 The typical farm worker earns about
$20,000 a year.
What causes earnings to
vary so much?
 Wages are governed by labor
supply and labor demand.
 Labor demand reflects the
marginal productivity of labor.
What causes earnings to
vary so much?
In equilibrium, each worker is
paid the value of his or her
marginal contribution (or MRP)
to the economy’s production of
goods and services.
Earning Determination
Market for
Physicians
W
W
Market for Fast
Food workers
W1
W2
0
L1
L
0
L2
L
Some Determinants of
Equilibrium Wages
 Compensating
 Human
differentials
capital
 Ability, effort, and chance
 Signaling
Compensating Differentials
 Compensating differentials
refer to
differences in wages that arises from
nonmonetary characteristics of different
jobs.
 Coal
miners are paid more than others with
similar levels of education.
 Night shift workers are paid more than day
shift workers.
 Professors are paid less than lawyers and
doctors.
Human Capital
Human capital is the accumulation
of investments in people.
The most important type of human
capital is education.
Human Capital
Education represents an expenditure
of resources at one point in time to
raise productivity in the future.
College graduates in the U.S. earn
about 65 percent more than workers
with a high school diploma.
Average Annual earnings by
Educational Attainment
1978
1998
High school, no college
$31,847
$28,742
College graduates
$52,761
$62,588
+66 percent
+118 percent
High school, no college
$14,953
$17,898
College graduates
$23,170
$35,431
+55 percent
+98 percent
Men
Percent extra for college grads
Women
Percent extra for college grads
An Alternative View of
Education: Signaling
Firms
use educational attainment as
a way of sorting between high-ability
and low-ability workers.
It
is rational for firms to interpret a
college degree as a signal of ability.
Wages above Equilibrium
 Minimum-wage
laws
 Market power of labor unions
 Efficiency wages
Efficiency Wages
The theory of efficiency wages holds that a
firm can find it profitable to pay high
wages because doing so increases the
productivity of its workers. High wages
may:
reduce worker turnover.
 increase worker effort.
 raise the quality of workers that apply for
jobs at the firm.

Economic Rent
For a factor market, economic rent is
the difference between the payments
made to a factor of production and the
minimum amount that must be spent
to obtain the use of that factor.
Economic Rent
Wage
A
SL
w*
DL = MRPL
B
Economic Rent
0
L*
Number of Workers
Land Rent
Price
($ per
acre)
Supply of Land
s2
s1
Economic
Rent
Economic
Rent
D2
D1
Number of Acres
Tax Incidence and Elasticity
Tax reduces
supply
1. When demand is more
elastic than supply...
Price
Supply
Price buyers pay
Price without tax
3. ...than on consumers.
Tax
Price suppliers
receive
0
Demand
2. ...the
incidence of
the tax falls more
heavily on suppliers...
Quantity
Incidence of Tax on Land
Price
($ per
acre)
Supply of Land
P
Rent without Tax
D
Number of Acres
Incidence of Tax on Land
Price
($ per
acre)
Supply of Land
All the tax is
borne by the
land supplier.
Price tenants
pay
Tax
Price landlords
receive
D
Rent after Tax
Number of Acres
Capital
 In economic theory, capital is one of the triad
of productive inputs (land, labor, and capital).
Capital consists of plant, equipment, and
inventory.
 In accounting and finance, capital means the
total amount of money subscribed by the
shareholder-owners of a corporation, in return
for which they receive shares of the company’s
stock.
Return on Capital
ROC＝Earnings/Invested Capital
In September 2003, Rentex Company bought a
bulldozer for $100,000 and rent it to an engineering
company. In September 2004, Rentex will receive a
payment of $20,000 for rent. How much is the ROC?
ROC=20,000/100,000
=0.20=20%
Return on Capital
If Rentex agrees to be paid in 2006 for the three
years’ rent and requires the same ROC be
maintained. How much should be the payment?
100,000× (1+0.2)3
=100,000×1.728=172,800
Payment=72,800
Present Value
Present value is today’s value for an asset
that yields a stream of income over time.
Valuation of such time streams of returns
requires calculating the present worth of
each component of the income, which is
done by applying a discount rate (or
interest rate) to future incomes.
Present Value
NCF
PV 
t
(1  r )
PV = present value
NCF = Net cash flow in the future
r = interest rate or discount rate
t = time period
Present Value
Somebody offers to sell you a bottle of
wine that matures in exactly 2 years and
can then be sold for exactly $11. Assuming
the market interest value is 5%, at most
how much should you pay for the wine
today?
PV=11/(1+0.05)2 =9.98
Present Value
Suppose Bull Company has sold three
bulldozers to different companies at
$100,000 each. However, one will pay the
sum in 2004, another in 2005, and the
other in 2007. If the interest rate is 20%,
what are the present values of the three
payments?
Present Value
PV1=100,000/(1+0.20)=$83,333
PV2=100,000/(1+0.20)2=$69,444
PV3=100,000/(1+0.20)4=$48,225
Value of a Firm
Suppose a company can earn $30
million a year and it is an ongoing
entity. The risk-adjusted discount
rate is 5%. What’s the value of the
firm?
Value of a Firm
T
1
2
Value of a Firm 

 ... 
2
T
(1  r1 ) (1  r2 )
(1  rT )
1
t

t
t 1 (1  rt )
T
Value of a Ongoing Firm
With Constant Returns


 ...

Value of a Firm 
2
(1  r ) (1  r )


(1  r )


1
r
1
(1  r )
Value of a Firm
Suppose a company can earn $30
million a year and it is an ongoing
entity. The risk-adjusted discount rate
is 5%. What’s the value of the firm?

$30，
000，
000
Value of the Firm  
r
0.05
 $600,000,000
Makeup of Personal Income
 Labor
earnings (wages)
 Property income (rents, interests,
dividends)
 Governments transfer payments
Income Inequality
(Percent of National income)
Country Bottom Second
Fifth
Fifth
USA
5.2
10.5
Japan
10.6
14.2
France
7.2
12.6
UK
6.6
11.5
China
5.9
10.2
Malaysia
4.5
8.3
Mexico
3.6
7.2
India
8.1
11.6
Middle
Fifth
15.6
17.6
17.2
16.3
15.1
13.0
11.8
15.0
Fourth
Fifth
22.4
22.0
22.8
22.7
22.2
20.4
19.2
19.3
Top
Fifth
46.3
35.6
40.2
43.0
46.6
53.8
58.2
46.1
Lorenz Curve
Percent of Income
100
80
Curve of absolute equality
60
40
Actual
distribution of
Chinese income
20
0
20
40
60
Percent of People
80
Curve of
100 absolute
inequality
Gini Coefficient
C
Percent of Income
100
80
Gini Coeffecient 
60
Shaded Area
Area of ABC
S
40
20
A
0
20
40
60
Percent of People
80
B
100
Gini Coefficient
 China’s
Gini in 2000 is 0.458.
 Ginis of successful economies range from
0.30 to 0.40.
 Countries of two low a Gini tend to
stagnate for lack of incentive.
 Too high a Gini means a serious inequality
of income distribution.
Market Equilibrium
MR=MC
Profit
Maximization
Market for
Goods
Goods &
Services sold and Services
Firms
Least-Cost
Rule
MU1/ P1 = MU2 /P2
Goods &
Services
bought
Utility
Maximization
Households
Inputs for
production
MPL/ PL = MPK /PK
Market for
Factors
of Production
Labor, land,
Income
and capital Determination
P=MRP
Pareto Efficiency
Pareto efficiency is a situation in which
no reorganization or trade could raise the
utility or satisfaction of one individual
without lowering the utility or satisfaction
of another individual.
Under certain limited conditions, perfect
competition leads to Pareto (or allocative)
efficiency.
Pareto Efficiency
John’s
Utility
300
D
130
100
0
A and C are of Pareto efficiency.
C
170
A
B
100 130
D is not available.
170
B is inefficient, for John’s
or Tom’s utility can be
improved without
hurting the other’s utility
300
Tom’s Utility
The Production
Possibilities Frontier
The production possibilities frontier (PPF)
is a graph showing the various
combinations of output that the economy
can efficiently produce given the available
factors of production and technology.
Quantity of
Computers
Produced
The Production
Possibilities Frontier
D
3,000
C
2,200
2,000
1,000
0
A
PPF
B
300
600 700
1,000
Quantity of
Cars Produced
Concepts Illustrated by the
Production Possibilities Frontier
Efficiency
Tradeoffs
Opportunity Cost
Economic Growth
Market Efficiency vs.
Market Failures
Recall that: Adam Smith’s “invisible
hand” of the marketplace leads selfinterested buyers and sellers in a market
to maximize the total benefit that society
can derive from a market.
But market failures
can still happen.
Market Failure
Market failure is an imperfection in
the price system that prevents an
efficient allocation of resources.
Important examples are externalities
and imperfect competition.
Externalities
Externalities are activities that affect others
for better or worse, without those others
paying or being compensated for the activity.
Externalities exist when private costs or
benefits do not equal social costs or benefits.
 The two major species are external
economies and external diseconomies.
External Economies
External economies (also called positive
externalities) are situations in which
production or consumption yields positive
benefits to others without those others
paying.
Examples:
 Immunizations
 Education
 Research
into new technology
External Diseconomies
External diseconomies (also called negative
externalities) are situations in which
production or consumption imposes
uncompensated costs on other parties.
Examples:
 Pollutions
 Cigarette
smoking
 Loud stereos in an apartment building
Internalizing Externalities
 Taxes are the primary tools used
to internalize negative
externalities.
 Subsidies are the primary tools
used to internalize positive
externalities.
Pigovian Taxes
Pigovian taxes are taxes enacted to
correct the effects of a negative
externality. Such taxes are named
after Arthur Pigou, an early advocate
of their use.
Tradable Pollution Permits
Tradable pollution permits allow the
voluntary transfer of the right to
pollute from one firm to another.
 A market
for these permits will eventually
develop.
 A firm that can reduce pollution at a low
cost may prefer to sell its permit to a firm
that can reduce pollution only at a high cost.
The Equivalence of Pigovian
Taxes and Pollution Permits
Pigovian Tax
Pollution Permits
Price of
Pollution
Price of
Pollution
P
0
P
Pigovian
tax
1. A Pigovian
tax sets the
price of
pollution...
Supply of
pollution permits
Demand for
pollution rights
Q
2. ...which, together
with the demand curve,
determines the quantity
of pollution.
Quantity of
Pollution
Demand for
pollution rights
0
2. ...which, together
with the demand curve,
determines the price
of pollution.
Q
Quantity of
Pollution
1. Pollution
permits set
the quantity
of pollution...
The Coase Theorem
The Coase Theorem states that if private
parties can bargain without cost over the
allocation of resources, then the private
market will always solve the problem of
externalities on its own and allocate
resources efficiently.
Transactions Costs
Transaction costs are the costs
that parties incur in the process
of agreeing to and following
through on a bargain.
Why Private Solutions
Do Not Always Work
Sometimes the private solution
approach fails because transaction
costs can be so high that private
agreement is not possible.
Why Private Solutions
Do Not Always Work
The market fails to allocate resources
efficiently when property rights are
not well-established (i.e. some item of
value does not have an owner with the
legal authority to control it).
Production and
Distribution
Production and Distribution
Digital tech lowers production costs
Digital tech lowers distribution costs
Examples
 Tape
recorder lowers production, but not
distribution costs
 AM radio broadcast lowers distribution
costs, not reproduction costs
Make Lower Distribution
Costs Work for You
Information is an experience good
Must give away some of your content in
order to sell rest
Can use product line/versioning
 National Academy
of Sciences Press
 Easy to read, hard to print
Demand for Repeat Views
Give away all your content, but only once
Music, books, video have different use
patterns
Children
 Barney:
free videos
 Disney: sued day care centers
Adults
Demand for Similar Views
Free samples direct customers back to
you
Playboy
McAfee Associates
 $5
million in first year
 $3.2 billion market value by 1997
 Half of virus protection market
Demand for
Complementary Products
Give away index and sell content
 Wall
Street Journal, New York Times,
Economist give away index
Free content, organization/index is what
matters
 Farcast
sells current awareness
Lower Reproduction Costs
Perfection isn’t as important as
commonly thought
Choosing Terms and
Conditions
Revenue = price x quantity
More liberal terms and conditions
 Increases
price
 Decreases quantity sold
Simple Model
y = amount consumed
x = amount sold
p(y) = demand, assume zero cost
Baseline case: max p(y)y
More liberal
a
p(y) with a>1
 y = bx with b < 1
Analysis
Max ap(y) x
Max (a/b) p(y)y
Conclusion: y the same, profits depend
on a/b
Assignment
Review Chapter 12 and 15
Answer questions on P224, 246, and
263
Preview Chapter 20 and 21
Thanks
Indifference Curves and MRS
C
MRS  
F
C
（Units）
C
dC
MRS  lim 

F 0
F
dF
B
A
E
△C
△F
D
U3
U2
U1
F(Units)
Budget Line
C
（Units）
(M/PC) = 40
Pc = $2
Pf = $1
M = $80
A
Budget Line: Pf F + Pc C = M
B
30
D
20
E
C
M / Pc
Slope  

F
M / Pf
Pf
1


Pc
2
10
G
0
20
40
60
80 = (M/PF)
F（Units）
Consumers’ Choice
C
（Units）
Pc = $2
Pf = $1
M = $80
40
D
A
B is the optimum choice
B
U3
U2
U1
0
80
Budget Line
F（Units）
Marginal Utility and
Consumers’ Choice
MU F (F )  MU c (C )
F
MU c

C
MU F
F
dF
PC
MRS 

 F
C dC
P
MU c
PC
 F
F
MU
P
Equal Marginal Principle
PF
PC

MU F
MU c
P1
P2
P3
PN


 ... 
1
2
3
MU
MU
MU
MU N
Equal Marginal Principle
Constraint=$20
Hot dog price=$2.5
MU of
Units per hot dogs
game
(MUH )
1
20
2
15
MUH /PH
8
6
Coke price=$2
MU of
Cokes
(MUc )
60
40
MUc /Pc
30
20
3
12.5
5
20
10
4
5
10
7.5
4
3
16
8
8
4
6
5
2
4
2
The Theory of Optimization
Budget=$2,000 TV ad price=$400 Radio ad price=$300
Number of ads
1
2
3
4
5
6
Increase in units sold
MBTV
MBRadio
400
360
300
270
280
240
260
225
240
150
200
120
The Theory of Optimization
Budget=$2,000 TV ad price=$400 Radio ad price=$300
Number of ads
1
2
3
4
5
6
Increase in units sold
MBTV
MBRadio
400/400=1.00 360/300=1.20
300/400=0.75 270/300=0.90
280/400=0.70 240/300=0.80
260/400=0.65 225/300=0.75
240/400=0.60 150/300=0.50
200/400=0.50 120/300=0.40
Isoquants and MRTS
K
MRTS  
L
K 5
△K
K
dK
MRTS  lim 

L0
L
dL
4
3
△L
2
Q3 =90
Q2 =75
1
Q1 =55
1
2
3
4
5
L
Marginal Rate of
Technical Substitution
 Assume the output quantity is
constant, then:
MPL (L)  MPK (K )
MPL
K

 MRTS
MPK
L
Isocost Line
Assume inputs are labor (L) and capital (K)
and wage and capital price are w and r
respectively, then:
C  wL  rK
C w
K  L
r r
Isocost Line
K
(Units)
(C/r) = 40
r = $2
w = $1
C = $80
A
Isocost Line: K= 40 – 0.5L
B
30
D
20
E
K
C/r
Slope 

L
C/w
w
1
 
r
2
10
G
0
20
40
60
80 = (C/w)
L (Units)
Least-Cost Rule
K
（Units）
For output Q1, point A is of
least cost
K2
A
K1
K3
Q1
C0
L2
L1
C1
L3
C2
L（Units）
Least-Cost Rule
K
（Units）
B
K2
A
K1
C2
L2
L1
Q1
C1
L（Units）
Least-Cost Rule
MPL (L)  MPK (K )
MPL
K

 MRTS
MPK
L
K
w

L
r
MPL
w

MPK
r
MPL
MPK

w
r
Profit Maximization
Revenue, Cost
and Profit($)
TC
TR
π
0
Output
Profit Maximization
Revenue($)
MR
TR
dTR(Q )
MR＝f ' (TR) 
dQ
0
Quantity
Profit Maximization
Cost($)
TC
MC
MC＝f ' (TC ) 
0
dTC (Q )
dQ
Quantity
Profit Maximization
Revenue, Cost
and Profit($)
TC
TR
A
B
0
q1
MR=MC
π
Output
Profit Maximization
 (Q )  TR(Q )  TC (Q )
d (Q ) dTR(Q ) dTC (Q )


0
dQ
dQ
dQ
MR (Q )  MC (Q )  0
MR (Q )  MC (Q )
Marginal Revenue Product
MRPL  MR  MPL
Q
TP
MR, P
MC
ATC
D
AP
MP
L
MR
Q
Value of Marginal Product
VMPL  P  MPL
Q
P
TP
MC
ATC
P = AR = MR
AP
MP
L
Q
Q
MRP of Labor
MRPL
($)
90
MRPL
0
1
2
3
4
5
6
7
8
9
L
MRP and Profit Maximization
To maximize profit, the competitive,
profit-maximizing firm hires workers up
to the point where the MRP equals the
wage—the marginal factor cost (MFC).
MRP  MFC
MRPL  w
MRP and Profit Maximization
MRP, w
A
Market
wage
MRPL= P×MPL = d
0
L
MRP and Profit Maximization
If MRPL > w,
hire more labor.
If MRPL < w,
hire less labor.
If MRPL = w,
it is a profit maximizing amount of labor
MRP and Profit Maximization
 ( L)  PQ( L) Q( L)  W  L
d ( L) dP dQ
dQ


Q  P 
W  0
dL
dQ dL
dL

 dQ
dP
Q  dQ  P dL  W


dTR dPQ
dP
MR 

Q
P
dQ
dQ
dQ
MR  MP  MRP  w
MRP and Profit Maximization
 ( L)  P  Q ( L)  W  L
d ( L)
 dQ ( L) 
 P
W  0

dL
 dL 
 dQ ( L ) 
P
W

 dL 
P  MP  W  VMP