Download Production Function - National Bureau of Economic Research

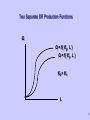
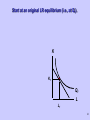
Production Function
 Qt=ƒ(inputst)
 Qt=output rate
 inputt=input rate
 where is technology?
Production Function
Q=ƒ(Kt,Lt)
Qt
Kt
 Firms try to be on the surface of the PF.
 Inside the function implies there is
waste, or technological inefficiency.
Lt
1
Difference between LR and SR
 LR is time period where all inputs can be varied.
 Labor, land, capital, entrepreneurial effort, etc.
 SR is time period when at least some inputs are fixed.
 Usually think of capital (i.e., plant size) as the fixed input, and labor
as the variable input.
2
LR production function as many SR production
functions.
Long Run: Q = f (K,L)
 Suppose there are two different sized
plants, K1 and K2.
 One Short Run:
Q = f ( K1,L) i.e., K fixed at K1
 A second Short Run:
Q = f ( K2,L) i.e., K fixed at K2


Show this graphically
3
Two Separate SR Production Functions
Q
Q = f( K2, L )
Q = f( K1, L )
K2 > K1
L
4
What Happens when Technology Changes?
This shifts the entire production function, both in the SR and in
the LR.
Technology Changes
Q
TP after computer
TP before computer
L
6
SR Production Function in More Detail
 Express this in two dimensions, L
and Q, since K is fixed.
 Define Marginal Product of Labor.
 Slope is MPL=dQ/dL
 Identify three ranges
Qt=ƒ(Kfixed,Lt)
I
II
III
Q
 I: MPL >0 and rising
 II: MPL >0 and falling
 III: MPL<0 and falling
L
7
Where Diminishing Returns Sets In
 As you add more and more variable
inputs to fixed inputs, eventually
marginal productivity begins to
fall.
 As you move into zone II,
diminishing returns sets in!
 Why does this occur?
Q
I
II
L
8
Why Diminishing Returns Sets In
 Since plant size (i.e., capital) is fixed,
labor has to start competing for the
fixed capital.
 Even though Q still increases with L
for a while, the change in Q is smaller.
Q
I
II
L
9
Define APL and MPL
 Average Product = Q / L
 output per unit of labor.
 frequently reported in press.
 Marginal Product = dQ/dL
 output attributable to last unit of labor used.
 what economists think of.
10
Average Productivity Graphically
 Take ray from origin to the SR
production function.
 Derive slope of that ray
Q=Q1
L=L1
 Thus,
Q/L =Q1 /L1
Q
Q=f(KFIXED,L)
Q1
Q
L
L1
L
11
Average Productivity Graphically
 APL rises until L2
 Beyond L2 , the APL begins to fall.
 That is, the average productivity
rises, reaches a peak, and then
declines
Q
Q=f(KFIXED,L)
Q2
Q/L
L
L2
APL
L2
12
Average & Marginal Productivity
 There is a relationship between the productivity of the average worker, and
the productivity of the marginal worker.
 Think of a batting average.
 Think of your marginal productivity in the most recent game.
 Think of average productivity from beginning of year.
 When MP > AP, then AP is RISING
 When MP < AP, then AP is FALLING
 When MP = AP, then AP is at its MAX
13
Average Productivity Graphically
Q
 MPL rises until L1
 Beyond L1 , the MPL begins to
fall.
 Look at AP
i. Until L2, MPL >APL and thus APL
rises.
ii. At L2, MPL=APL and thus APL peaks.
iii. Beyond L2, MPL<APL and thus APL
falls.
L1
L
L2
Q/L
MPL
L1 L2
APL
14
Intuitive explanation
 Anytime you add a marginal unit to an average unit, it either pulls the
average up, keeps it the same, or pulls it down.
 When MP > AP, then AP is rising since it pulls it the average up.
 When MP < AP, then AP is falling since it pulls the average down.
 When MP = AP, then AP stays the same.
 Think of softball batting average example.
15
LR Production Function
Qt
Kt
Isoquants
(i.e.,constant
quantity)
Lt
16
Define Isoquant
Different combinations of Kt and Lt which generate the
same level of output, Qt.
Isoquants & LR Production Functions
ISOQUANT MAP
 Qt = Q(Kt, Lt)
 Output rate increases as you move to higher
isoquants.
 Slope represents ability to tradeoff inputs while
holding output constant.

K
Marginal Rate of Technical Substitution.
 Closeness represents steepness of production
hill.
Q3
Q2
Q1
L
18
Slope of Isoquant
 Slope is typically not constant.
 Tradeoff between K and L depends
on level of each.
 Can derive slope by totally
differentiating the LR production
function.
 Marginal rate of technical
substitution is –MPL/MPK
Kt
Q
Lt
19
Extreme Cases
 No Substitutability
 Perfect Substitutability
K
K
Q2
Q
Q1
2
Q1
L
Inputs used in fixed
proportions!
L
Tradeoff is constant
20
Substitutability
Low Substitutability
High Substitutability
K
K
Q1
Q1
L
Slope of Isoquant
changes a lot
L
Slope of Isoquant
changes very little
21
Isoquants and Returns to Scale
Returns to scale are cost savings associated with a firm
getting larger.
Increasing Returns to Scale
 Production hill is rising quickly.
 Lines on the contour map get
closer with equal increments in
Q.
K
Q=40
Q=30
Q=20
Q=10
L
23
Decreasing Returns to Scale
 Production hill is rising slowly.
 Lines on the contour map get
further apart with equal
increments in Q.
K
Q=40
Q=30
Q=20
Q=10
L
24
How Can You Tell if a PF has IRS, DRS, or CRS?
 It is possible that it has all three, along various ranges of
production.
 However, you can also look at a special kind of function, called a
homogeneous function.
 Degree of homogeneity is an indicator returns to scale.
25
Homogeneous Functions of Degree 
 A function is homogeneous of degree k
 if multiplying all inputs by , increases the dependent variable by
 Q = f ( K, L)
 So,  • Q = f(K,  L) is homogenous of degree k.
 Cobb-Douglas Production Functions are homogeneous of degree 
+
26
Cobb-Douglas Production Functions
Q=A•K •L
is a Cobb-Douglas Production Function
 Degree of Homogeneity is derived by increasing all the inputs by 
= A • ( K) • ( L) 
 Q = A •   K •   L
 Q =   A • K • L
  Q


27
Cobb-Douglas Production Functions
 This is a Constant Elasticity Function
 Elasticity of substitution s = 1
 Coefficients are elasticities
 is the capital elasticity of output, EK
 is the labor elasticity of output, E L
 If Ek or L <1 then that input is subject to Diminishing Returns.
 C-D PF can be IRS, DRS or CRS
 if  +  1, then CRS
 if  + < 1, then DRS
 if  + > 1, then IRS
28
Technical Change in LR
 Technical change causes isoquants to shift inward
 Less inputs for given output
 May cause slope to change along ray from origin
 Labor saving
 Capital saving
 May not change slope
 Neutral implies parallel shift
29
Technical change
 Labor Saving
 Capital Saving
K
K
L
L
30
Lets now turn to the Cost Side
What is Goal of Firm?
Define Isocost Line
 Put K on vertical axis, and L on
horizontal axis.
 Assume input prices for labor (i.e., w)
and capital (i.e., r) are fixed.
 Define: TC=w*L + r*K
 Solve for K:
r*K= TC-w*L
K=(TC/r) - (w/r)*L
Isocost Line
K
TC/r
Slope=-w/r
L
32
TC constant along Isocost line.
K
TC1/r
L
TC1/w
33
in TC parallel shifts Isocost
K
TC2/r
TC2 > TC1
TC1/r
L
TC1/w TC2/w
34
Change in input price rotates Isocost
K
w2 < w1
TC/r
L
TC/w1 TC/w2
35
Optimal Input Levels in LR
 Suppose Optimal Output level is
determined (Q1).
 Suppose w and r fixed.
 What is least costly way to
produce Q1?
K
Q1
L
36
Optimal Input Levels in LR
 Suppose Optimal Output level is
determined (Q1).
 Suppose w and r fixed.
 What is least costly way to produce Q1?
 Find closest isocost line to origin!
K
 Optimal point is point of allocative
efficiency.
K1
Q1
L1
L
37
Cost Minimizing Condition
 Slopes of Isoquant and Isocost are equal
Slope of Isoquant=MRTS=- MPL/ MPK
Slope of Isocost=input price ratio=-w/r
At tangency, - MPL/ MPK = -w/r
 Rearranging gives: MPL/w= MPK /r
 In words:
 Additional output from last $ spent on L = additional output from last $ spent on
K.
38
The LR Expansion Path
 Costs increase when output
increases in LR!
 Look at increase from Q1 to Q2.
 Both Labor and Capital adjust.
 Connecting these points gives the
expansion path.
K
expansion path
K2
K1
Q2
Q1
L
L1 L2
39
We can show that LR adjustment along the
expansion path is less costly than SR adjustment
holding K fixed!
Start at an original LR equilibrium (i.e., at Q1).
K
K1
Q1
L
L1
41
LR Adjustment
 LR adjustment:
 K increases (K1 to K2)
 L increases (L1 to L2)
 TC increases from black to blue isocost.
K
K2
K1
Q2
Q1
L1 L2
L
42
SR Adjustment
 SR adjustment.
 K constant at K1.
 L increases (L1 to L3)
 TC increases from black to white
isocost.
K
K1
Q2
Q1
L1
L3
L
43
LR Adjustment less Costly
 White Isocost (i.e., SR) is further from
the origin than the Blue Isocost (LR).
 Thus, the more flexible LR is less costly
than the less flexible SR.
K
K2
K1
Q2
Q1
L1 L2 L3
L
44
Impact of Input Price Change
 Start at equilibrium.
 Recall slope of isocost=K/L= -w/r
 Suppose w and optimal Q stays
same (i.e., Q1)
 Rotate budget line out, and then
shift back inward!
K
Q1
K1
L1
L
45
Decrease in wage leads to substitution
 Firms substitute away from capital (K1
to K2).
 Firms substitute toward labor (L1 to
L2)
 Pure substitution effect: a to b
 Maps out demand for labor curve
K
a
K1
b
K2
Q1
L1
L2
L
46
Derivation of Labor Demand from Substitution
Effect
 Wage falls
w
K
w1
a
K1
w2
b
K2
Q1
L1
L2
DL1
L
L1
L2
L
47
There is also a scale effect
 Scale effect is increase in output that
results from lower costs
 Scale effect: b-c
K
Q1
Q2
a
K1
c
b
L1
L
48
Scale Effect Shifts Demand
 Wage falls
w
K
w1
K1
c
a
w2
b
K2
DL2
Q1
L1
L2 L3
DL1
L
L1
L2 L3
L
49
Recall the Isocost Line
TC=w*L + r*K
Thus, TC=TVC+TFC
 Lets relate the cost relationships to the
production relationships.
 Recall the Law of Diminishing Returns.

50
Law of Diminishing Marginal Returns
 As you add more and more variable inputs (L) to your fixed inputs
(K), marginal additions to output eventually fall (i.e., MPL=
Q/L falls)
 What does this say about the shape of cost curves?
51
Marginal Productivity (MPL) and Marginal Cost (MC)





Look at how TC changes when output changes.
Assume w and r are fixed.
Since TC=w*L+r*K
then TC = w*L + r*K
How does K change in SR?
52
Changes in TC in SR must come from changes in
Labor.
TC = w* L
Divide through by change in Q (ie. Q)
TC/Q = w* (L/Q)
TC/Q = Marginal Cost = MC
What is MPL?
MPL=(Q/L)
 Thus: TC/Q = w* 1/(Q/L)
 This gives: MC=w/MPL





53
MC=w/MPL
Look at where Diminishing Returns sets in.
MC
MPL
MPL
L1
L
Q
54
MC=w/MPL
Substitute L1 into SR Production Function
Q1=f(KFIXED,L1)
MC
MPL
MC
MPL
L1
L
Q1
Q
55
Alternatively: TC and TP
Substitute L1 into SR Production Function
Q1=f(KFIXED,L1)
TC
Q
TC
MPL
L1
L
Q1
Q
56
Relationship between APL and AVC






TC=TVC + TFC
TC = w*L + r*K
Divide equation by Q to get average cost formula.
TC/Q = w*L/Q + r*K/Q
ATC = AVC + AFC
Thus, AVC=w*L/Q
57
AVC and APL
 AVC=w*L/Q
 Rearranging: AVC=w/(Q/L)
 Since Q/L=APL
AVC=w/APL
 Diagram is similar.
58
AVC=w/APL
Substitute L2 into SR Production Function
Q2=f(KFIXED,L2)
APL
AVC
AVC
APL
L2
L
Q2
Q
59
Put SR Cost Curves Together
Average Cost Curves
ATC
$
AVC
AFC
Q
61
Short Run Average Costs and Marginal Cost
$
ATC
MC
AVC
Q
62
Cost Curve Shifters
(Variable Cost Increases)
 A change in the wage shifts the
AVC and MC curves.
 Thus, the ATC curve also shifts
upward.
MC’ ATC’
$
AVC’
ATC
AVC
MC
Q
63
Cost Curve Shifters
(Fixed Cost Increases)
 An increase in price of capital
increases fixed costs, but not
variable costs.
 Thus, AVC and MC are fixed, but
ATC increases.
$
ATC’
MC ATC
AVC
Q
64
Costs in the LR
 Why did SR cost curves have the shape they did?
 Why do LR cost curves have the shape they do?
65
LR Total Costs Graphically
TC
Cost
CRS
DRS
IRS
Q
66
Why are there Economies of Scale?
 Specialization in use of inputs.
 Less than proportionate materials use as plant size
increase.
 Some technologies are not feasible at small scales.
67
Why do Diseconomies of Scale Set In?
 Eventually, large scale operations become more costly to
operate (i.e., they use more resources) due to problems of
coordination and control.
 e.g., red tape in the bureaucracy.
 Graphical Representation
68
Economies and Diseconomies of Scale
Assume Q increases 10 units for each isoquant
K
IRS
L
69
Economies and Diseconomies of Scale
Assume Q increases 10 units for each isoquant
K
DRS
IRS
L
70
Economies and Diseconomies of Scale
LRAC curve
Assume Q increases 10 units for each isoquant
K
$
DRS
DRS
IRS
CRS
CRS
IRS
L
QMES
Q
71
LRMC and LRAC Curves
LRAC and LRMC
 LRMC is TC/Q (i.e., change in
TC from a change in Q) when all
inputs are variable inputs.
 When LRMC is above LRAC, it
pulls the average up, and viceversa.
$
LRMC LRAC
Q
73
Relating SR to LR curves
Relationship between SR ATC and LRAC curves.
 At Q1, the SR plant size which gives
ATC1 is least costly.
$
ATC1
LRAC
Q
Q1
75
Relationship between SR ATC and LRAC curves.
 At Q1, the SR plant size which gives
ATC1 is least costly.
 SR ATC is tangent to LRAC at one
point.
$
ATC1
LRAC
Q
Q1
76
Relationship between SR ATC and LRAC curves.
$
ATC1
LRAC
 At Q1, the SR plant size which gives
ATC1 is least costly.
 SR ATC is tangent to LRAC at one
point.
 Tangency is not at minimum point of
ATC1.
Q
Q1
77
Adjustments in SR are still more costly than LR
 At Q2, the SR plant size which gives
ATC1 is no longer least costly.
$
ATC1
LRAC
atc1
lrac1
Q
Q2
78
Adjustments in SR are still more costly than LR
 At Q2, the SR plant size which gives
ATC1 is no longer least costly.
 Optimal move would be to larger
plant size!
$
ATC1
LRAC
atc1
lrac1
Q
Q2
79
LRAC is lower “envelope” of family of SRATC
curves
$
ATC1
ATC2
ATC3
LRAC
Q
Q1
Q2=QMES
Q3
80
SRMC and LRMC
$
LRMC
SRMC1
SRMC3
SRMC2
LRAC
SRATC3
SRATC1
SRATC2
q1
q2
q3
q
81